Предмет: Геометрия,
автор: galchonokryzhyk212
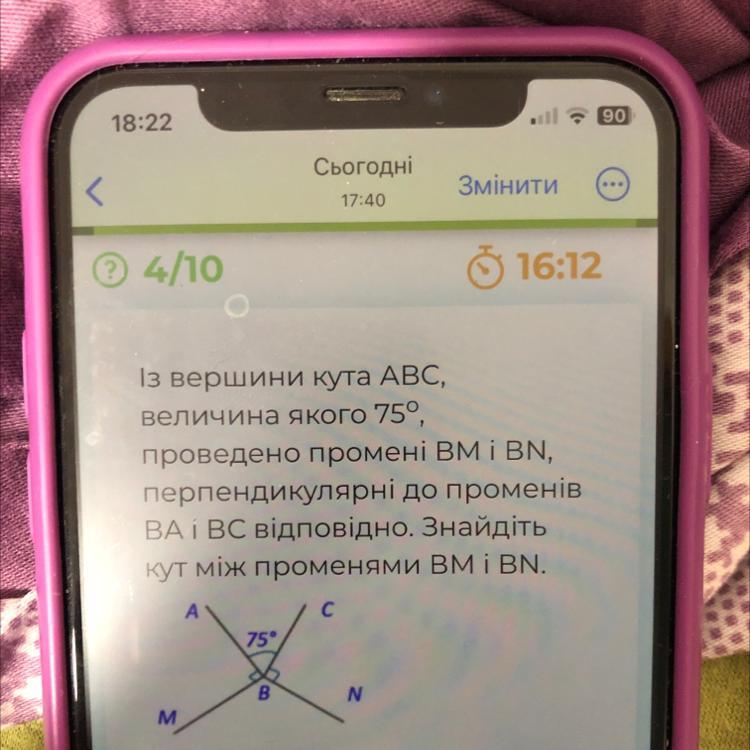
Із вершини кута ABC,
величина якого 75°,
проведено промені ВМ і BN,
перпендикулярні до променів
BA і ВС відповідно. Знайдіть
кут між променями ВМ i BN,
Приложения:
Ответы
Автор ответа:
1
Ответ:
Згідно з теоремою про суму кутів трикутника, сума кутів трикутника ABC дорівнює 180°. Оскільки кут ABC дорівнює 75°, то кути BAC і BCA дорівнюють 180° - 75° = 105°.
Оскільки промені ВМ і BN перпендикулярні до променів BA і ВС відповідно, то кути ABM і ABN дорівнюють 90°.
Отже, кут між променями ВМ і BN дорівнює різниці кутів BAC і ABN, тобто 105° - 90° = **15°**.
Відповідь: 15°.
**Альтернативний спосіб розв'язання**
Оскільки промені ВМ і BN перпендикулярні до променів BA і ВС відповідно, то кут між ними дорівнює 90°. Отже, кут між променями ВМ і BN дорівнює 90° - 75° = **15°**.
Цей спосіб розв'язання заснований на тому, що кут між двома перпендикулярними променями дорівнює 90°..
galchonokryzhyk212:
Дякую вам велике
Похожие вопросы
Предмет: Геометрия,
автор: yarunakostechko
Предмет: Литература,
автор: rartem2609
Предмет: ОБЖ,
автор: dadadadada145
Предмет: Русский язык,
автор: Sezimaketova
Предмет: Право,
автор: senozenskijaroslav