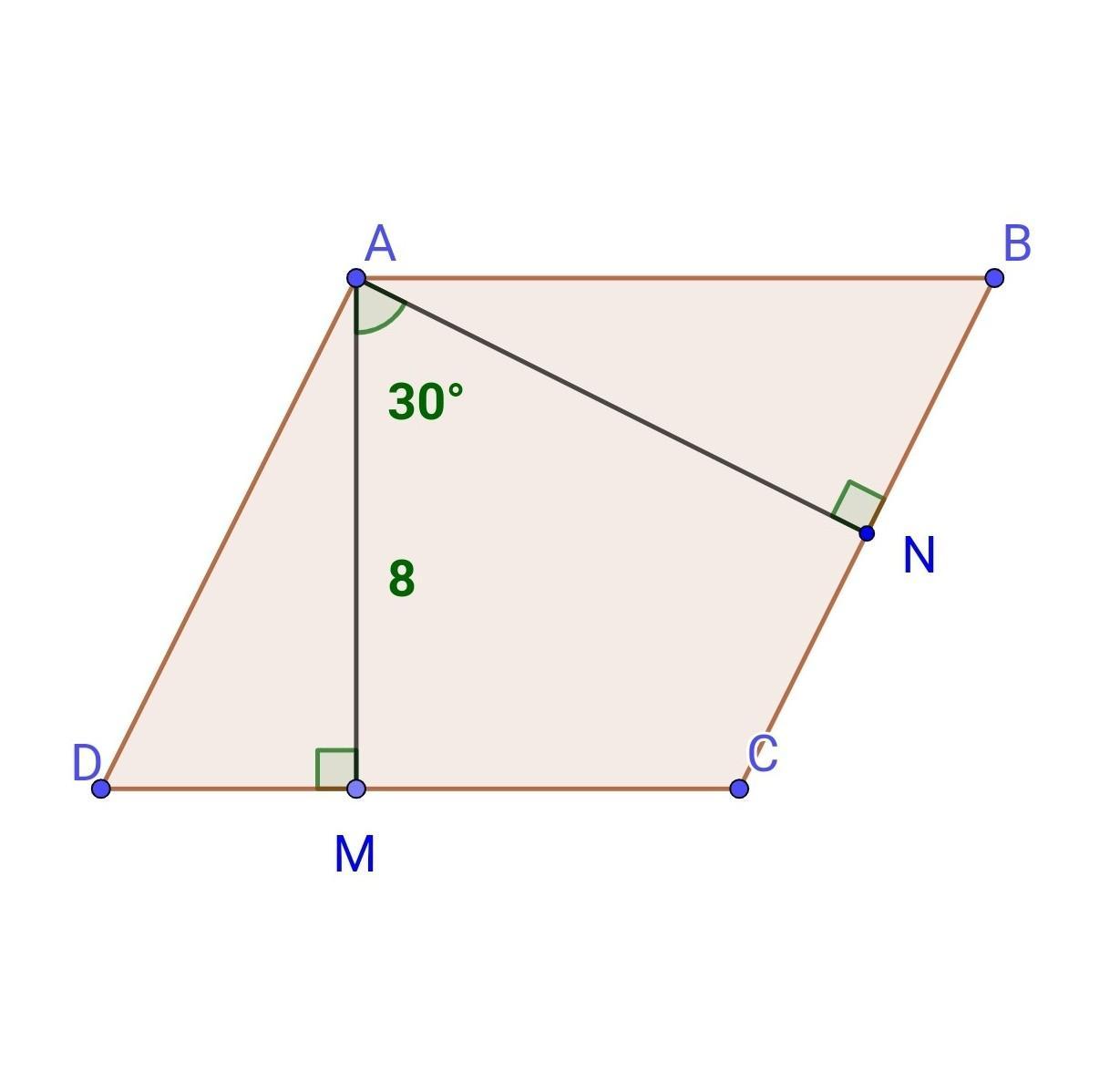
У ромбі ABCD з вершини тупого кута A проведено висоти AM і AN до сторін DC і BC відповідно. Знайдіть периметр ромба, якщо AM = 8 см, ∠MAN = 30°.
Ответы
Ответ:
Периметр ромба дорівнює 64 см
Объяснение:
ABCD з вершини тупого кута A проведено висоти AM і AN до сторін DC і BC відповідно. Знайдіть периметр ромба, якщо AM = 8 см, ∠MAN = 30°.
За умовою ABCD - ромб, AM і AN - його висоти, AM⟂DC, AN⟂BC, AM = 8 см, ∠MAN = 30°.
Знайдемо периметр ромба.
1.
У чотирикутнику ANCM:
∠C = 360° - (∠MAN - ∠ANC - ∠AMC) = 360° - (30° + 2•90°) = 150°
2.
За властивістю сусідніх кутів ромба маємо:
∠D + ∠C = 180°
∠D = 180° - ∠C = 180° - 150° = 30°
3.
Розглянемо прямокутний трикутник AMD(∠M=90°).
∠D = 30°, AM = 8 см.
Катет АМ лежить проти кута 30°, тому за властивістю він дорівнює половині гіпотенузи. Отже, гіпотенуза AD = 2 • AM = 2 • 8 = 16(см)
4.
Так як у ромба всі сторони рівні, то його периметр обчислюється за формулою:
Р = 4 • а
де а - сторона ромба.
Р = 4 • 16 = 64 (см)
#SPJ1