Завдання 4. Звести до канонічного вигляду рівняння кривої другого по-
рядку за допомогою переносу початку координат. Визначити тип,
параметри кривої та побудувати її. Побудувати стару та нову си-
стеми координат та криву: y^2 - 7x + 8y + 9= 0
Ответы
Ответ:
Щоб звести рівняння кривої до канонічного вигляду за допомогою переносу початку координат, треба виконати наступні кроки:
1. Переносимо квадратичний член в одну частину рівняння:
y^2 + 8y = 7x - 9.
2. Додамо до обох частин рівняння постійний доданок, який рівний коефіцієнту при x, поділеному на 2 і піднесеному до квадрату:
y^2 + 8y + (8/2)^2 = 7x - 9 + (8/2)^2.
3. Спрощуємо це рівняння:
y^2 + 8y + 16 = 7x - 9 + 16.
4. Переносимо все в ліву частину рівняння:
y^2 + 8y + 16 - 7x + 9 - 16 = 0.
5. Згруповуємо подібні члени:
y^2 + 8y - 7x + 9 = 0.
Тепер ми отримали рівняння кривої в канонічному вигляді. Щоб з'ясувати тип та параметри цієї кривої, необхідно провести аналіз квадратичного члена.
В даному випадку, ми маємо квадратичний член по y з коефіцієнтом 1 та лінійний член з коефіцієнтом 8. За типом це є парабола.
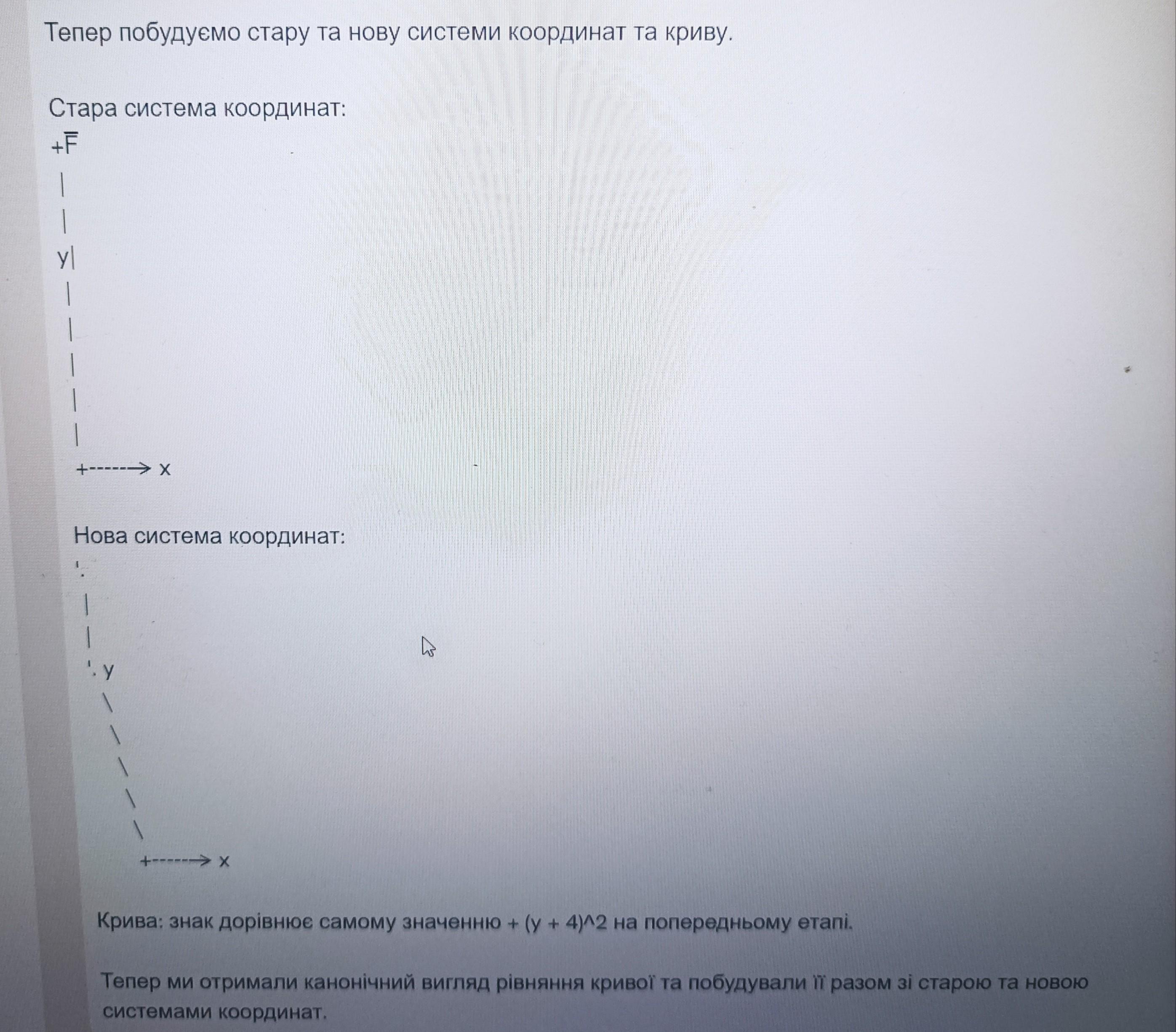
Тепер побудуємо стару та нову системи координат та криву:
Стара система координат: