Question

Сторона основи правильної піраміди 11см, а двогранни кут при ребрі основи - 45° Знайти відстань від центра основи до бігно грані пераміди та площу повной поверкий

Answer 1

Ответ:

Высота правильной четырёхугольной пирамиды равна 1,5 см

Пошаговое объяснение:

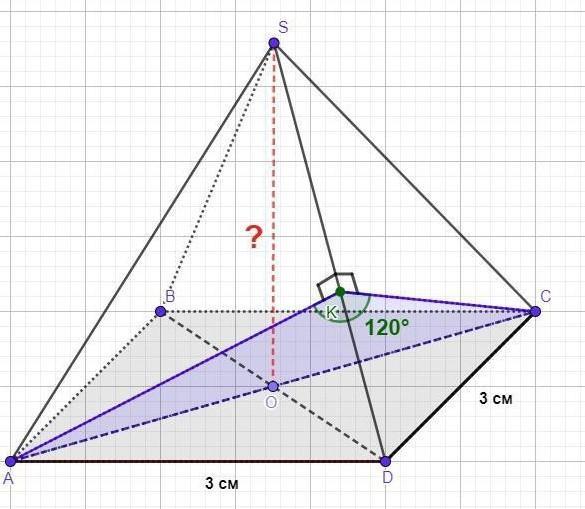
Определите высоту правильной четырёхугольной пирамиды, в которой сторона основания равна 3 см, двугранный угол между боковыми гранями равен 120°.

ДАНО: SABCD - правильная четырёхугольная пирамида. АВ = 3 см.

∠((ASD),(CSD))=120°

НАЙТИ: SO - ?

Правильная четырехугольная пирамида — это многогранник, у которого одна грань (основание пирамиды) квадрат, а остальные (боковые) грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.

Так как пирамида правильная, то:

АВ=ВС=СD=АD=3 см;

Диагональ АС = а√2 = АВ√2= 3√2 см;

ОD=АС/2 = см - как половина диагонали квадрата;

Проводим высоты к боковому ребру SD из вершин А и С пирамиды. Так как ΔASD = ΔCSD, то высоты сойдутся в одной точке К. (т.к. ΔАКD=ΔСКD по 1 признаку. КD-общая, АD=СD, ∠АDК=∠СDК)

Итак, АК⊥SD и СК⊥SD. Тогда ∠АКС - линейный угол двугранного угла, по условию ∠АКС=120°.

1) Рассмотрим ΔАКС.

По теореме косинусов находим АК.

АС²=АК²+КС²-2·АК·АС·cos∠AKC

cos∠AKC = cos120° = -1/2, КС=АК, АС=3√2 ⇒

(3√2)²=АК²+АК²-2АК²·(-1/2)

3АК²=18

АК²=6

АК=√6 см

2) Рассмотрим ΔАКD (∠K=90°).

По теореме Пифагора находим катет КD.

КD²= АD²-АК²=3²-(√6)²=9-6=3

КD=√3 см

3) Рассмотрим ΔАSС (∠K=90°).

По теореме Пифагора находим катет SK.

SK²=AS²-AK²

Учитывая, что SK=SD-KD, а AS=SD, получаем:

(SD-KD)²=SD²-АК²

(SD-√3)²=SD²-(√6)²

SD²-2√3·SD+3=SD²-6

-2√3·SD=-9

cм

3) Рассмотрим ΔSOD (∠О=90°).

По теореме Пифагора находим катет SO.

SO²=SD²-OD²

см

Высота SO равна 1,5 см

#SPJ5