Предмет: Геометрия,
автор: evilxq0
Дан треугольник ABC. EF- средняя линия треугольника. AE=4, AC=10, CF=5. AE=EB, CF=BF. Найти периметр треугольника BEF.
Приложения:
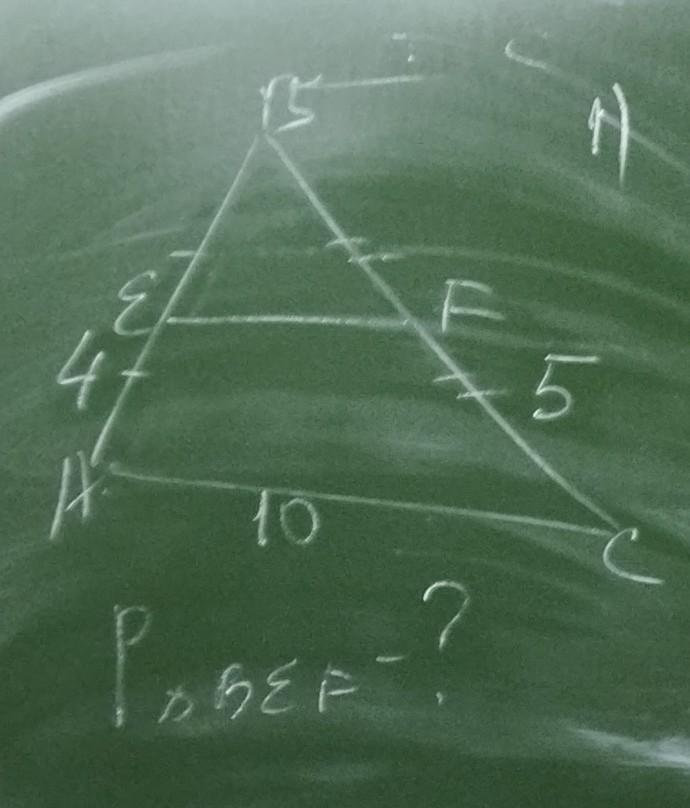
Ответы
Автор ответа:
1
Ответ:
14
Объяснение:
по теореме о средней линии имеем, что она равна половине параллельной стороны, то есть EF=АС/2=10/2=5;
BE=AE=4, BF=CF=5, отсюда Pabc=4+5+5=14
evilxq0:
Спасибо большое
Автор ответа:
1
Відповідь:
14
Пояснення:
Если CF=BF, то сторона BC треугольника ABC равна 5*2=10.
Поскольку стороны АС и ВС равны 10, то треугольник АВС - равнобедренный.
Поскольку ЕF - средняя линия треугольника АВС, то треугольник BFE также равнобедренный, а сторона BF=FE=5.
Значит АЕ=ЕВ=4, ВF=5, FE=5.
Соответственно периметр треугольника BFE равен 5+5+4=14.
Спасибо
Похожие вопросы
Предмет: Українська мова,
автор: vojcenkorita311
Предмет: Физика,
автор: terehovustin72
Предмет: Алгебра,
автор: abakhytbek49
Предмет: Русский язык,
автор: matriowka
Предмет: Математика,
автор: torgansasa400