Предмет: Математика,
автор: amirkaznaetwse
493. Вычислите: 1 1 3 + 3 + 1 3 +. 10 раз + 1 3 1 2 11_ 22 8 раз 2) (100 + 1 100 + 1 100 +...+ 15 раз 1 100
Приложения:
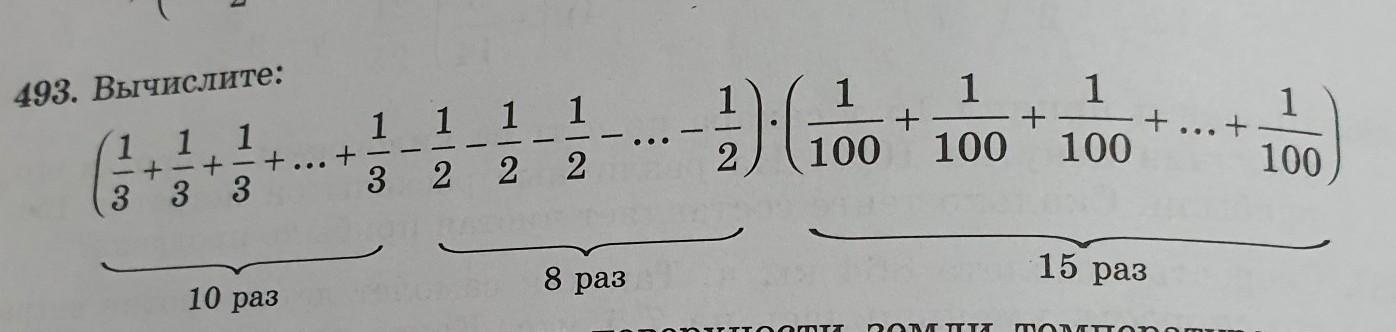
Ответы
Автор ответа:
1
Ответ и Пошаговое объяснение:
Требуется вычислить
Информация. Сумма n чисел а равна n·a.
Решение. Вычислим значение выражения:
#SPJ1
Похожие вопросы
Предмет: Українська мова,
автор: prochuvailenko2010
Предмет: Другие предметы,
автор: PlashkalotlPP
Предмет: История,
автор: ze240946
Предмет: Геометрия,
автор: andreishestakov2003
Предмет: Физика,
автор: Аноним