Question

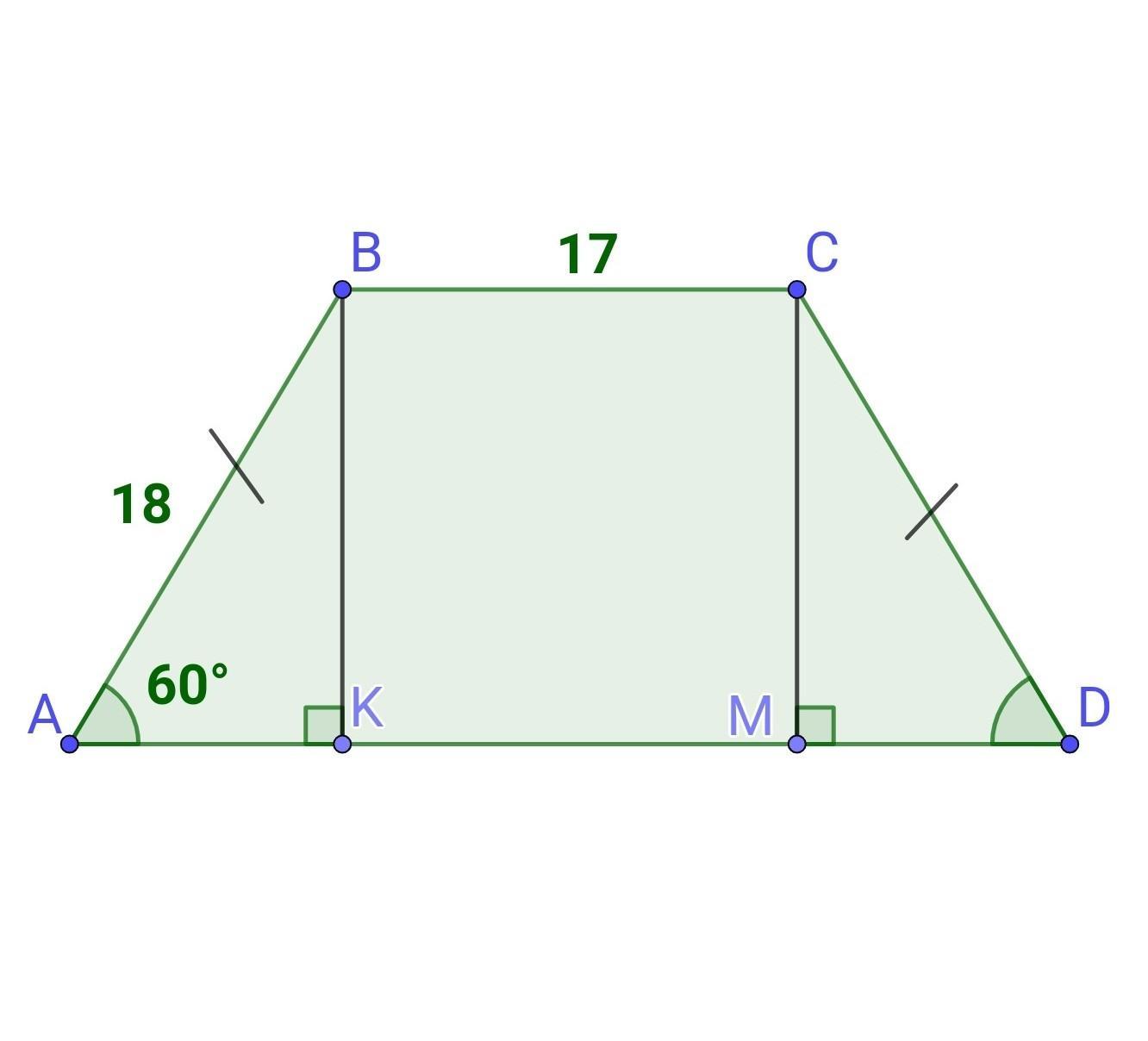
Один з кутів рівнобічної трапеції дорівнює 60°, менша основа 17см, а бічна сторона 18см. Знайдіть периметр трапеції.​

Answer 1

Ответ:

Периметр трапеції дорівнює 88 см.

Объяснение:

Один з кутів рівнобічної трапеції дорівнює 60°, менша основа 17см, а бічна сторона 18см. Знайдіть периметр трапеції.

Нехай ABCD дана трапеція, BC||AD, AB=CD=18 см, BC=17 см, ∠А=60°.

Знайдемо периметр трапеції.

1.

Проведемо дві висоти ВК і СМ.

Розглянемо прямокутний трикутник АВК(∠К=90°).

За теоремою про суму гострих кутів прямокутного трикутника маємо:

∠А +∠АВК = 90°

Тоді ∠АВК = 90° - ∠А = 90° -60° = 30°.

АК = ½ • АВ = ½ • 18 = 9(см) - як катет, що лежить напроти кута 30°.

2.

Розглянемо △ABK і △DCM

• ∠A=∠D - як кути при основі рівнобічної трапеції
• AB=CD - як бічні сторони рівнобічної трапеції

Отже, △ABK=△DCM за гіпотенузою і гострим кутом.

Тоді АК = MD = 9 (см)

3.

KBCM - прямокутник. KM = BC = 17 см - як протилежні сторони прямокутника.

4.

AD = AK + KM + MD = 9 + 17 + 9 = 35(см) - за аксиомою вимірювання відрізків.

5.

Знайдемо периметр трапеції, як суму всіх її сторін:

Р(ABCD) = AB + BC + CD + AD = 18 + 17 + 18 + 35 = 88 (см).

Відповідь: Р (ABCD) = 88 см

#SPJ1