Предмет: Алгебра,
автор: tgtffctvyj6
((a - b)/(a ^ 2 + ab) - a/(ab + b ^ 2)) / ((b ^ 2)/(a ^ 3 - a * b ^ 2) + 1/(a + b))
Приложения:
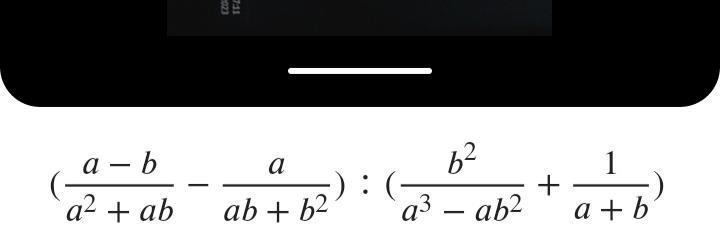
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Немецкий язык,
автор: nataliahatsevic
Предмет: Геометрия,
автор: 2058v32emii
Предмет: Химия,
автор: andrijdonec7
Предмет: Математика,
автор: billcipher191