Предмет: Алгебра,
автор: taraksergey
Допоможіть з виразом будь ласка, треба спростити по діям.
(y^2/(x^3-xy^2 )+1/(x+y)) :((x-y)/(x^2+xy)-x/(xy+y^2 ))
Приложения:
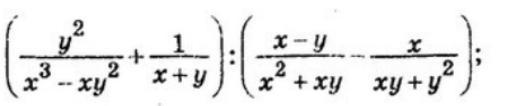
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Литература,
автор: kusakbaevagulzihan
Предмет: Физика,
автор: AleksandrVoskoboev18
Предмет: Алгебра,
автор: ritakotegova1
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: abregov009