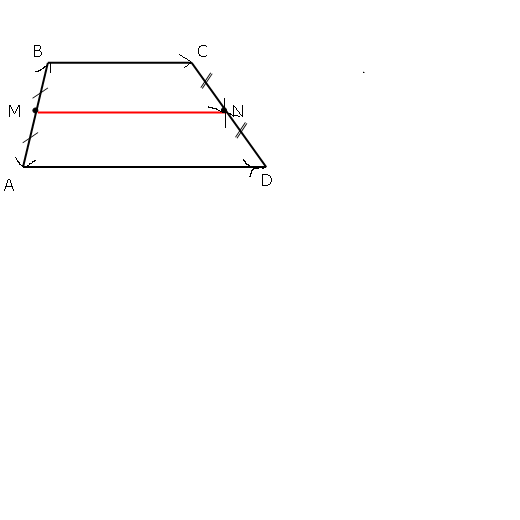
нужно доказать, что средняя линия трапеции равна полусумме оснований.
Ответы
Доказательство:
Рассмотрим трапецию ABCD c основаниями AD и BC , высотой BH и площадью S. Докажите, что S=1/2(AD+BC)*BH.
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S=S(ABD)+S(BCD).
Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DF за основание и высоту треугольника BCD. Тогда S(ABD)=1/2AD*BH, S(BCD)=1/2*CB*DF. Т.к. DF=BH, тогда S(BCD)=1/2*CB*BH.
S=1/2AD*BH+1/2 BC*BH=1/2(AD+BС)*ВН.
Теорему о средней линии трапеции докажем с помощью веторов.
Пусть MN - средняя линия трапеции ABCD (основания AD и BC).
По правилу многоугольника MN=MB+BC+CN и MN=MA+AD+DN.
Сложив эти равенства получим:
2MN=(MB+MA)+(BC+AD)+(CN+DN)
Но M и N - середины сторон AB и CD. Поэтому MB+MA=0, CN+DN=0. Следовательно 2MN=AD+BC, откуда выводим, что MN=0,5(BC+AD).
Сорри за корявость рисунка)