Question

найти объем, нужно полное решение

Answer 1

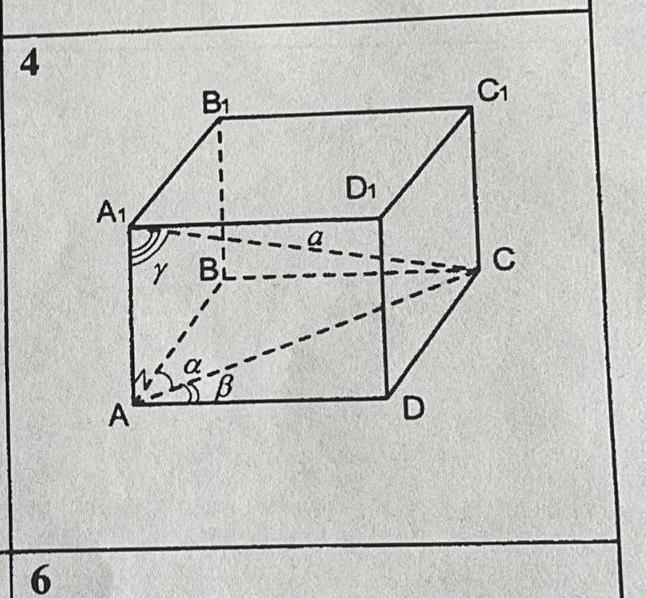
Будем считать, что надо определить объём прямого параллелепипеда.

Диагональ основания АС = a*sin γ, а высота Н =  АА1 = a*соs γ.

Теперь находим стороны основания (а это параллелограмм) по теореме синусов, с учётом, что угол ACD равен α, а синус угла ADC равен синусу (α + β).

AC/sin(α + β) = AD/sin α.

Отсюда находим сторону AD = AC *sin α /sin(α + β) = a*sin γ *sin α /sin(α + β).

Аналогично находим сторону АВ = CD.

AC/sin(α + β) = AВ/sin β.

AB = AC *sin β /sin(α + β) = a*sin γ *sin β /sin(α + β).

Площадь So параллелограмма равна произведению его сторон на синус угла между ними.

So = AB*AD*sin(α + β) =

    = (a*sin γ * sin β /sin(α + β)) * (a*sin γ * sin α /sin(α + β)) * sin(α + β) =

   = a²*sin² γ * sin α * sin β / sin(α + β).

Теперь находим объём V параллелепипеда.

V = So*H = (a²*sin² γ * sin α * sin β / sin(α + β)) * a*соs γ =

  = (a³*sin² γ * cos  γ * sin α * sin β / sin(α + β)).