208. Решите уравнение: a) x² + x = 0; (25x)2 4
г) 1 - 4x =
д) 2(3x - 4)2 = 7(6x + +44/17);
6) x²-x/2 = 0;
B) x² = 2x = 3x² + 4x;
e) 5(2x - 3)² = 15(3-2x). - 3 5
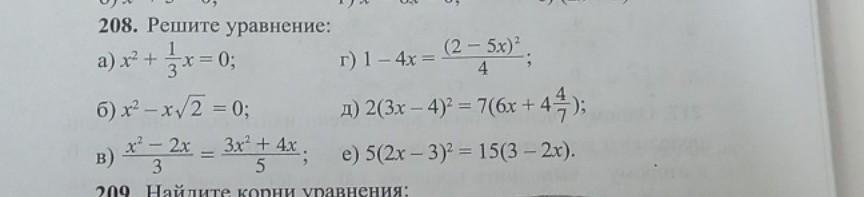
Ответы
Ответ:
Давайте розв'яжемо кожне з поданих рівнянь окремо:
а) x² + x = 0
Це квадратне рівняння можна спростити:
x(x + 1) = 0
Отже, рівняння має два корені:
x₁ = 0
x₂ = -1
б) (25x)² - 4
Розглянемо це як квадрат різниці:
(25x)² - 2² = (25x - 2)(25x + 2)
Отже, рівняння розкладається на два підрівняння:
25x - 2 = 0
25x + 2 = 0
Розв'язуємо кожне з них:
25x₁ = 2 => x₁ = 2/25
25x₂ = -2 => x₂ = -2/25
г) 1 - 4x = 0
Вирішимо це рівняння:
1 - 4x = 0
-4x = -1
x = 1/4
д) 2(3x - 4)² = 7(6x + 44/17)
Спершу розкриємо дужки:
2(9x² - 24x + 16) = 7(6x + 44/17)
Помножимо обидві сторони на 17 (щоб позбавитися від дробів):
34(9x² - 24x + 16) = 7(102x + 44)
Розкриємо дужки:
306x² - 816x + 544 = 714x + 308
Переносимо все на одну сторону рівняння:
306x² - 816x + 544 - 714x - 308 = 0
306x² - 1530x + 236 = 0
Тепер розв'яжемо це квадратне рівняння. Можна спростити націле націле, поділивши кожен член на 2:
153x² - 765x + 118 = 0
Знайдемо корені цього рівняння, використовуючи квадратну формулу.
6) x² - x/2 = 0
Це рівняння можна спростити, взявши x за спільний множник:
x(x - 1/2) = 0
Отже, рівняння має два корені:
x₁ = 0
x₂ = 1/2
в) x² = 2x = 3x² + 4x
Це рівняння виглядає неправильно. Воно містить рівність, яка не підходить до виразу. Будь ласка, перевірте формулювання задачі.
е) 5(2x - 3)² = 15(3 - 2x) - 3/5
Спершу розкриємо дужки:
5(4x² - 12x + 9) = 15(3 - 2x) - 3/5
Розкриємо дужки:
20x² - 60x + 45 = 45 - 30x - 3/5
Помножимо обидві сторони на 5 (щоб позбавитися від дробу):
100x² - 300x + 225 = 225 - 150x - 3
Переносимо все на одну сторону рівняння:
100x² - 300x + 225 - 225 + 150x + 3 = 0
100x² - 150x + 3 = 0
Зараз розв'яжемо це квадратне рівняння.