3.23 только 2 пример
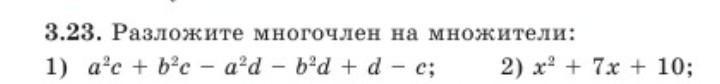
Ответы
Ответ:
2) х2 + 7х + 10
х2 +5х+2х+10
х*(х+5) + 2(х+5)
(х+5)*(х+2)
Ответ:
1) Для разложения многочлена \( a^{2} c+b^{2} c-a^{2} d-b^{2} d+d-c \) на множители, мы можем сгруппировать его члены следующим образом:
\( (a^{2} c - a^{2} d) + (b^{2} c - b^{2} d) + (d - c) \)
Затем, мы можем применить факторизацию по общему множителю для каждой группы:
\( a^{2} c - a^{2} d = a^{2} (c - d) \)
\( b^{2} c - b^{2} d = b^{2} (c - d) \)
\( d - c = -(c - d) \)
Теперь мы видим, что \( c - d \) является общим множителем для всех трех групп. Мы можем вынести его за скобки:
\( a^{2} (c - d) + b^{2} (c - d) - (c - d) \)
Теперь у нас есть общий множитель \( (c - d) \), который мы можем вынести за скобки:
\( (c - d) (a^{2} + b^{2} - 1) \)
Таким образом, многочлен \( a^{2} c+b^{2} c-a^{2} d-b^{2} d+d-c \) разлагается на множители как \( (c - d) (a^{2} + b^{2} - 1) \).
2) Многочлен \( x^{2}+7 x+10 \) уже является квадратным трехчленом. Мы можем попытаться разложить его на множители, используя метод разложения на множители квадратного трехчлена или применив формулу квадратного трехчлена. Однако, в данном случае, этот многочлен не разлагается на множители с целыми коэффициентами. Таким образом, \( x^{2}+7 x+10 \) не может быть разложен на множители с целыми коэффициентами.