Question

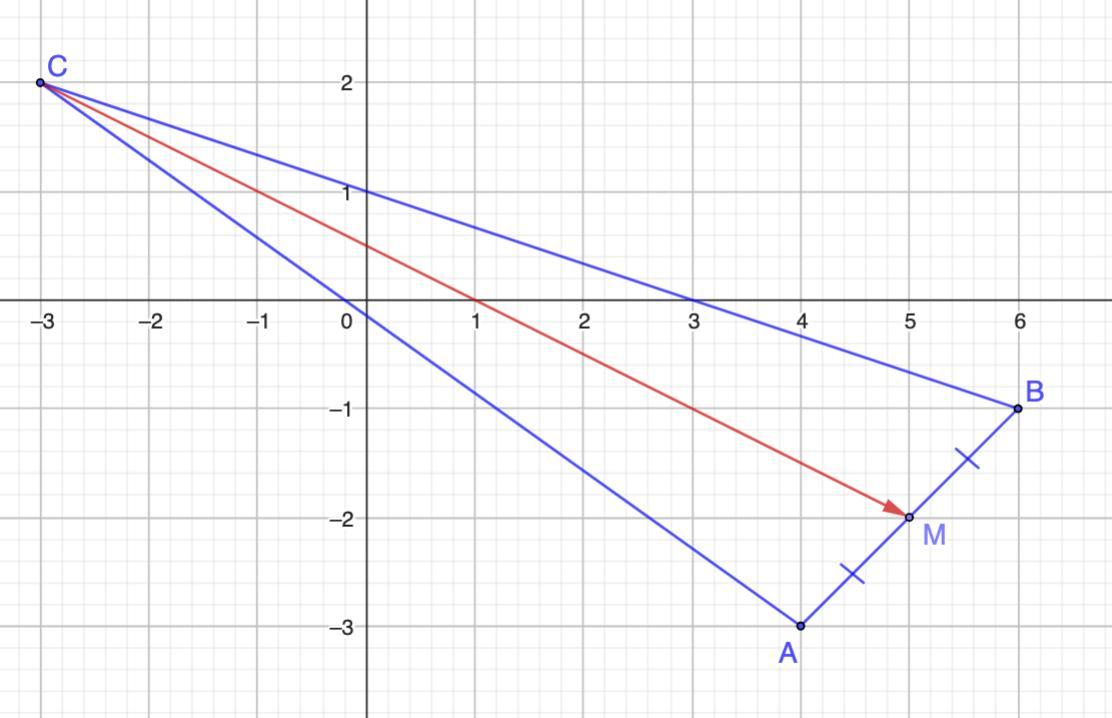
В трикутнику АВС вершини мають координати А(4;-3), В(6: -1), С(-3; 2). СМ медіана трикутника. Знайдіть координати вектора СМ.
​

Answer 1

Ответ:

Координаты   $\displaystyle \bf \overrightarrow{CM}(8; -4)$

Объяснение:

В треугольнике АВС вершины имеют координаты A(4; -3), B(6; -1), C(-3; 2). СМ - медиана треугольника. Найдите координаты вектора CM.

A(4; -3), B(6; -1)

СМ - медиана ΔАВС.

⇒ М - середина отрезка АВ.

• Координаты середины отрезка:

              $\boxed {\displaystyle \bf x=\frac{x_1+x_2}{2};\;\;\;\;\;y=\frac{y_1+y_2}{2} }$

$\displaystyle x_M=\frac{x_A+x_B}{2}=\frac{4+6}{2}=5\\ \\ y=\frac{y_A+y_B}{2}=\frac{-3-1}{2}=-2$

Координаты точки М(5; -2)

• Если А(х₁; у₁) и В(х₂; у₂), то координаты вектора АВ:

                    $\boxed {\displaystyle \bf \overrightarrow{AB}(x_2-x_1;\;\;\;y_2-x_1) }$

C(-3; 2);   М(5; -2).

$\displaystyle \bf \overrightarrow{CM}=(5-(-3); \;\;\;-2-2) = (8; -4)$

#SPJ1