Question

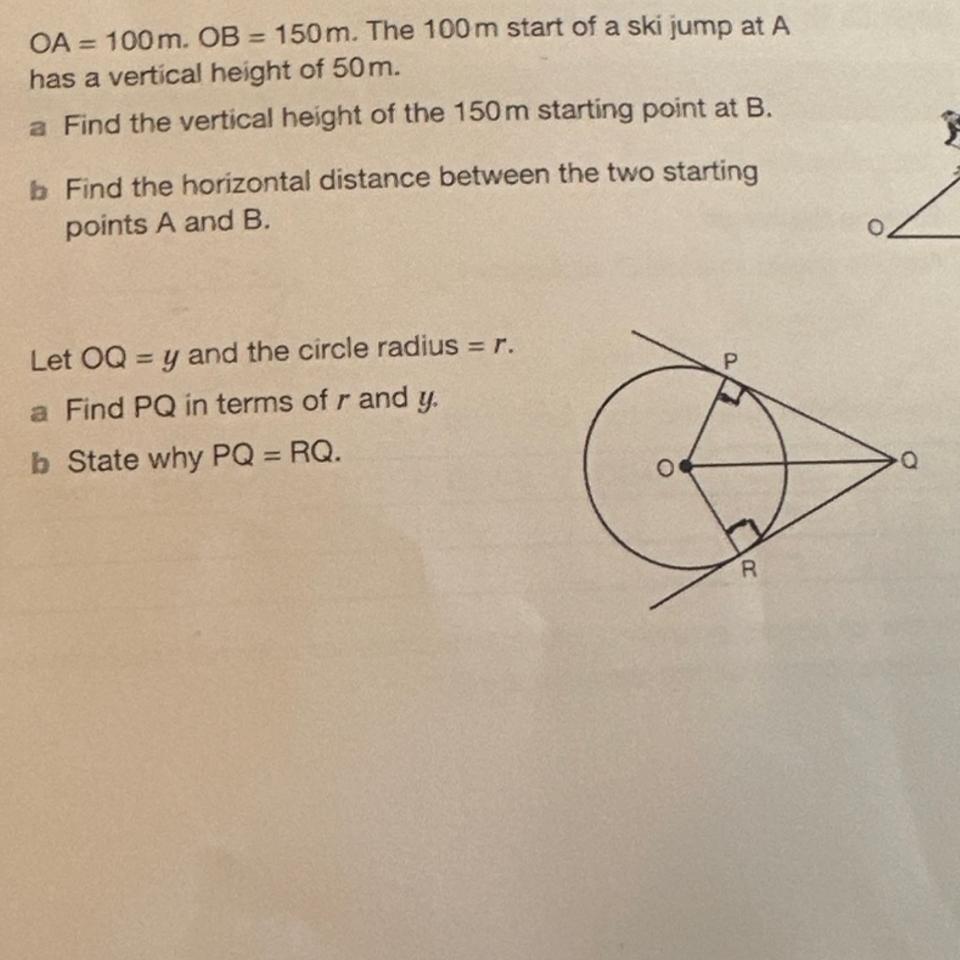
9 Let OQ = y and the circle radius = r.
a Find PQ in terms of r and y
b State why PQ = RQ.

Answer 1

Ответ:

a . √y²-r²

Пошаговое объяснение:

объяснения на фото ↑

Answer 2

I often used the services of a translator because my English is poor in mathematics. The way to solve the problem may not be the same as it is done in your country, but the essence should be clear

Пошаговое объяснение:

Let OQ = y and circle radius OP = r

a)

Consider triangle OPQ:

Since PQ is a tangent to a circle with center O, it means r ⊥ PQ (The tangent to the circle and the radius drawn to the point of tangency are mutually perpendicular)

Then triangle OPQ is right triangle (∠OPQ = 90°)

According to the Pythagorean theorem: OP² + PQ² = OQ²

Means:

$PQ^2=y^2-r^2\\\\PQ=\sqrt{y^2-r^2}$

b)

Since RQ is a tangent to a circle with center O, it means r ⊥ RQ (The tangent to the circle and the radius drawn to the point of tangency are mutually perpendicular)

Then the triangle ORQ is right-angled (∠ORQ = 90°)

Consider the right triangles OPQ and ORQ:

OR -- radius of the circle. According to the problem conditions OR = r

The radii of the circle are equal to each other, then OP = OR = r

The OQ side is general.

If the hypotenuse and leg of one right triangle are equal to the hypotenuse and leg of another, then such triangles are congruent:

Thus, triangles OPQ and ORQ are equal (OPQ = ORQ)

Since in equal triangles the sides are equal

Then PQ = RQ

Q.E.D.