Question

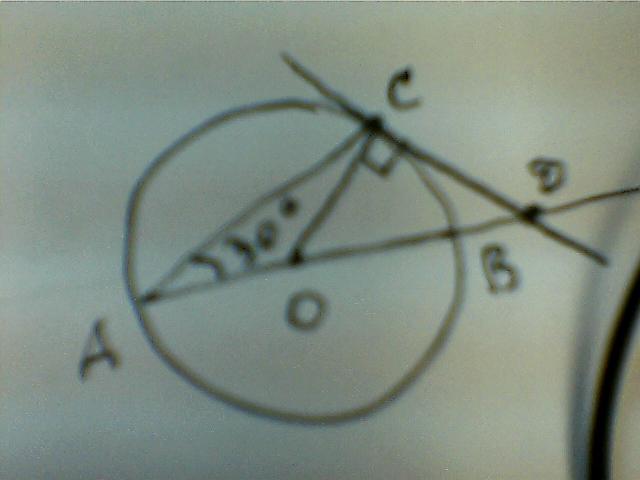
Угол между диаметром АВ и хордой АС равен 30°. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник ACD равнобедренный.С рисунком плз.Заранее спасибо

Answer 1

Угол СОВ - центральный, а угол САВ - вписанный. Опираются на одну и ту же дугу. 

Значит угол СОВ = 2*30 = 60 град

Тр-ик СОД - прямоуг, т.к. касательная СД перпендикулярна радиусу ОС.

Значит угол СДО = 90-60 = 30 град.

Получилось, что в тр-ке АСД: угол САД = углу СДА = 30 град

Значит тр-ик АСД - равнобедренный, что и требовалось доказать.