Question

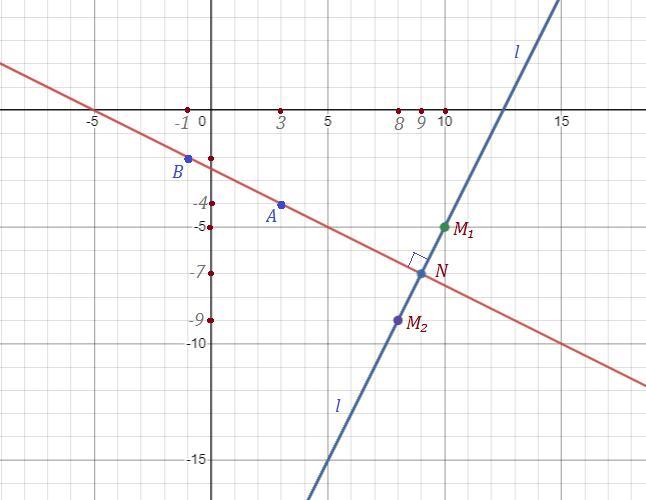
Знайти точку M1, симетричну точці M2 (8; −9) відносно прямої, що проходить через точки А(3;–4) та В(–1;–2).

Answer 1

Решение .

$\bf M_2(8;-9)\ \ ,\ \ A(3;-4)\ ,\ \ B(-1;-2)$

Прямая АВ :   $\bf \dfrac{x-3}{-1-3}=\dfrac{y+4}{-2+4}\ \ \Rightarrow \ \ \dfrac{x-3}{-4}=\dfrac{y+4}{2}\ \ \Rightarrow \ \ x+2y+5=0$    

Направляющий вектор прямой АВ равен   $\bf \overline{s}=(-4;2)$   или    $\bf \overline{s}=(2;-1)$

Прямая  $l$ , ортогональная прямой АВ , проходящая через точку М₂ :

$\bf 2\cdot(x-8)-1\cdot (y+9)=0\ \ \ \to \ \ \ \ \boldsymbol{l:\ 2x-y-25=0}$  

Точка пересечения АВ и $l$  :

$\left\{\begin{array}{lll}\bf x+2y=-5\\\bf 2x-y=25\ |\cdot 2\end{array}\right\ \ +\ \left\{\begin{array}{lll}\bf x+2y=-5\\\bf 5x=45\end{array}\right\ \ \left\{\begin{array}{lll}\bf 2y=-14\\\bf x=9\end{array}\right\ \ \left\{\begin{array}{lll}\bf y=-7\\\bf x=9\end{array}\right$

Точка  N(9;-7) является серединой отрезка  М₁М₂ .

Найдём координаты точки  М₁ .

$\bf 9=\dfrac{8+x}{2}\ \ ,\ \ 18=8+x\ \ ,\ \ x=10\\\\-7=\dfrac{-9+y}{2}\ \ ,\ \ -14=-9+y\ \ ,\ \ y=-5\\\\M_1(\, 10\, ;\, -5\ )$            

Ответ:  М₁( 10 ; -5 ) .