Question

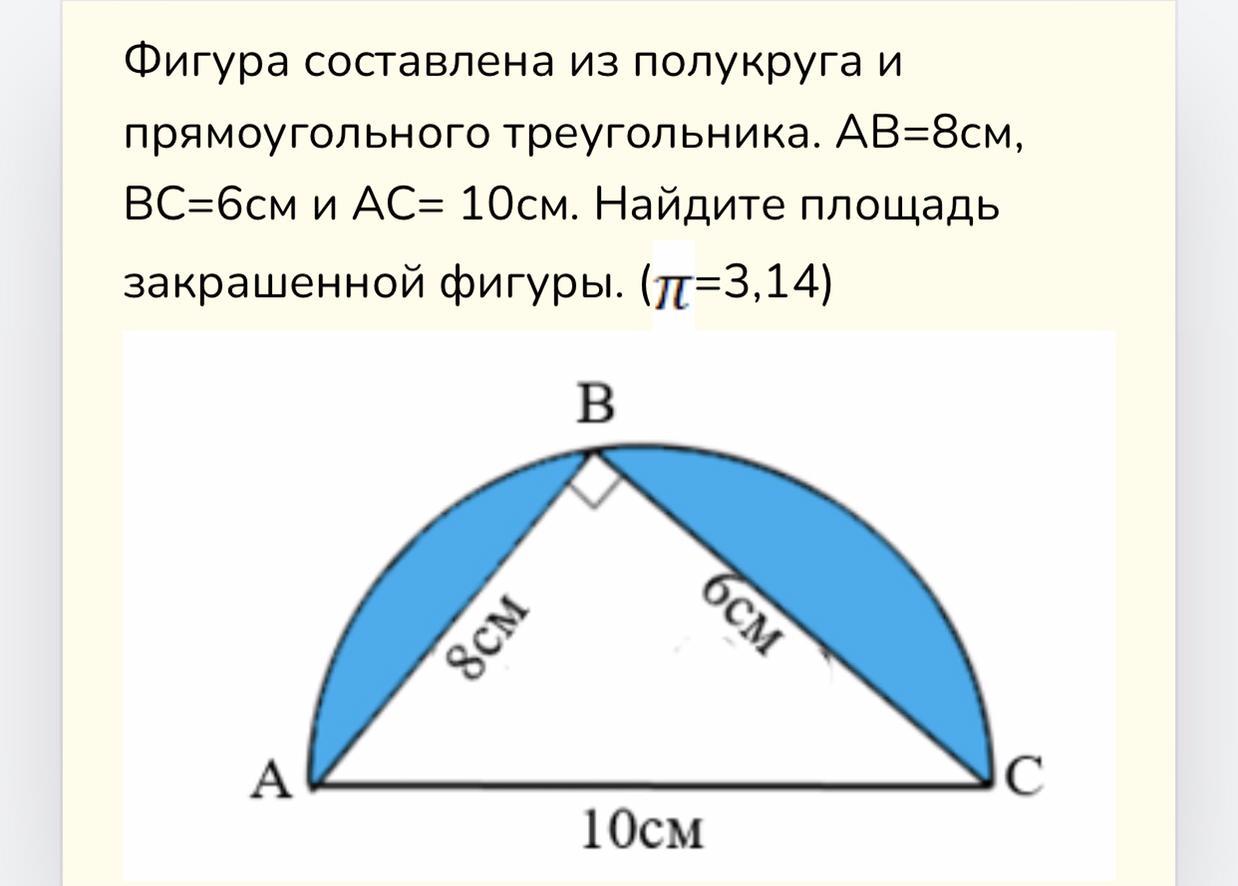
Фигура составлена из полукруга и прямоугольного треугольника. АВ=8см, ВС=6см и АC= 10см. Найдите площадь закрашенной фигуры. (Пи=3,14) (прошу ответьте как можно подробнее)

Answer 1

Ответ:

15,25 см².

Объяснение:

Фигура составлена из полукруга и прямоугольного треугольника АВ = 8см, ВС = 6см, АС = 10 см. Найти площадь закращенной части.

Чтобы найти площадь закрашенной части, надо из площади полукруга отнять площадь площадь прямоугольного треугольника.

Найдем площадь каждой фигуры.  На рисунке изображен ролукруг. Тогда гипотенуза АС является диаметром окружности. Найдем радиус

R = 10 : 2 = 5 cм.

Площадь круга определяется по формуле: S = π · R².

Тогда площадь полукруга

$S =\dfrac{1}{2} \pi R^{2} ;\\\\S =\dfrac{1}{2} \pi \cdot 5^{2} =\dfrac{1}{2} \pi \cdot 25 = 12,5 \pi$

Так как π ≈ 3,14, то

S ≈ 12,5 · 3,14 = 39,25 см².

$\begin{array}{r}\underline{\times\begin{array}{r}3\text{,}14 \\ 12\text{,}5\end{array}} \\ \underline{+\begin{array}{r}1570 \\ 628~ \; \\ 314~ \; \hspace{0.5em}\end{array}} \\ 39\text{,}250\hspace{0.6em}\end{array}$

Найдем площадь прямоугольного треугольника как полупроизведение катетов.

$S =\dfrac{1}{2} \cdot AB \cdot BC;\\\\S =\dfrac{1}{2} \cdot 8 \cdot 6 = 4\cdot 6 = 24$

Значит, площадь прямоугольного треугольника 24 см ².

И площадь заштрихованной части

39,25 - 24 = 15, 25 см².

#SPJ1