Предмет: Алгебра,
автор: rekviemtiktokovic
ДАЮ 100 БАЛІВ
!!ДУЖЕ ТЕРМІНОВО!!
розв'язання двох нерівностей (розбити
кожну нерівність на дві, розкриваючи знак модуля в залежності від знака х).
Приложения:

Ответы
Автор ответа:
2
Ответ:
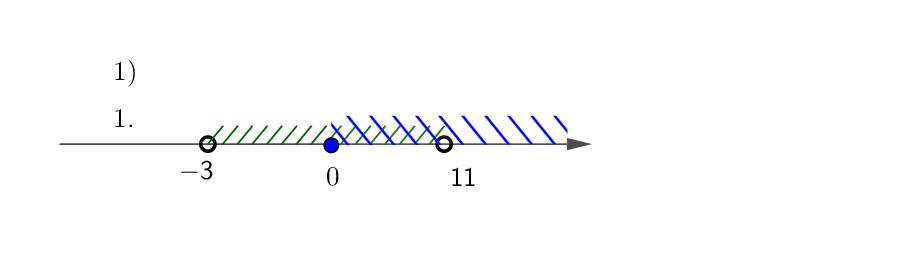
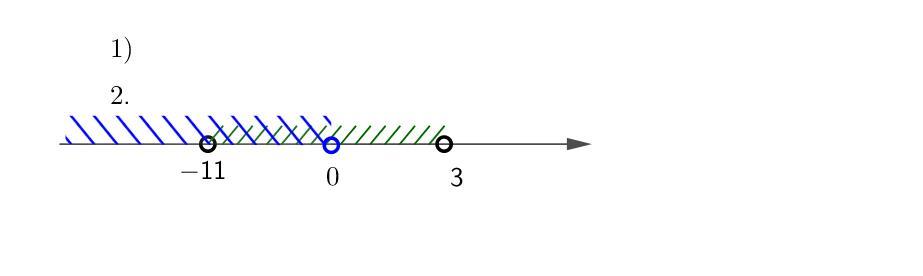
1)
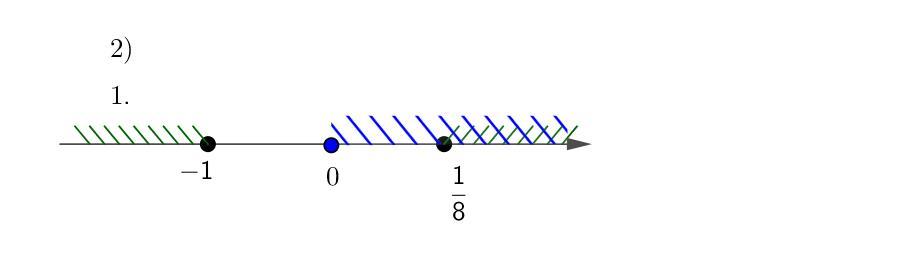
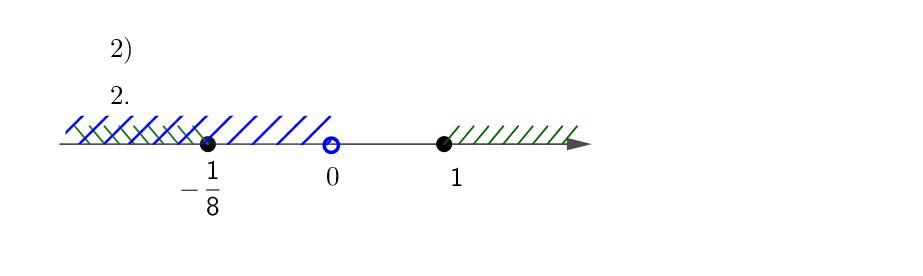
2)
Объяснение:
нерівність набуває вигляду
Нулі:
нерівність набуває вигляду
Нулі:
Відповідь:
---------------------------------
нерівність набуває вигляду
Нулі:
нерівність набуває вигляду
Нулі:
Відповідь:
Приложения:
rekviemtiktokovic:
Можеш ще будь-ласка зобразити графік
кожному випадку по бути графік?
Так
Я добавилa вложения
Похожие вопросы
Предмет: Литература,
автор: azelinska242
Предмет: Математика,
автор: d3898731
Предмет: Литература,
автор: rahubovska
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: mspuk