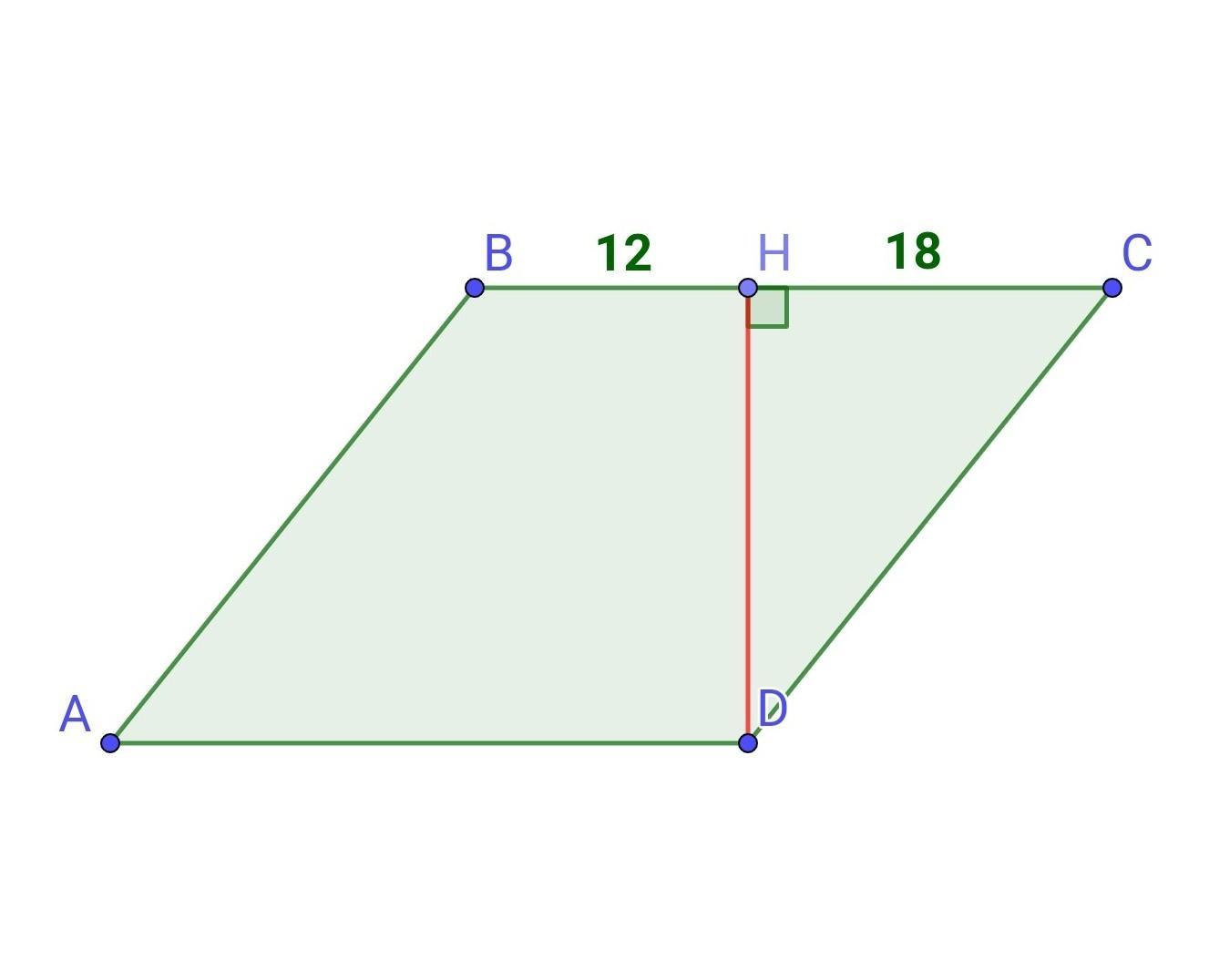
дано ромб ABCD у якому з вершини кута D до сторони BC проведеноперпендикуляр DH. BH=12см. HC=18 см. Визнач довжину перпендикуляра DH. Обчисли площу ромбо ABCD.
Ответы
Ответ:
Довжина DH = 24 см, площа ромба дорівнює 720 см ²
Объяснение:
Дано ромб ABCD у якому з вершини кута D до сторони BC проведеноперпендикуляр DH. BH=12см. HC=18 см. Визнач довжину перпендикуляра DH. Обчисли площу ромбо ABCD.
За умовою ABCD - ромб, DН⟂ВС, DH - висота. ВН=12 см, НС = 18 см.
Знайдемо DH і S(ABCD).
1) За властивістю ромба: АВ = ВС = СD = AD = BH + HC = 12 + 18 = 30 (см).
2) Розглянемо прямокутний трикутник HCD (∠H=90°).
Катет НС = 18 см, гіпотенуза СD = 30 см.
За теоремою Піфагора знайдемо катет DH.
DH² = CD² - HC² = 30² - 18² = (30-18)(30+18) = 12 • 48 = 576
DH = 24 (см)
2) Площа ромба дорівнює добутку його сторони на висоту, що проведена до цієї сторони:
S(ABCD) = BC • HD = 30 • 24 = 720 (см²)
Відповідь: DH=24 см, S(ABCD)=720 см²
#SPJ1