Предмет: Геометрия,
автор: lulurabl28
Дан куб ABCD A1B1C1D1 площадь поверхности, которого 48. Плоскость а проходит через точку М параллельно плоскости АВ1 С. Найдите периметр сечения куба плоскостью а. (точка M , находится между B и B1. по середине)
dnepr1:
А где находится точка М ???
днепр1 можете допомогти будь ласка
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба: S = 6 a²,
где S - площадь куба,
a - длина грани куба.
Подставим заданное значение S = 48.
48 = 6a², сокращаем обе части уравнения на 6.
а² = 48/6 = 8.
Сторона куба равна а = √8 = 2√2.
Плоскость АВ1 С пересекает грани куба по диагоналям d граней.
Диагональ d = a√2 = 2√2*√2 = 4.
Так как точка М находится на середине ребра, то параллельные линии сечения равны половинам диагоналей d.
Периметр сечения Р = 3*(4/2) 3*2 = 6 ед.
Приложения:
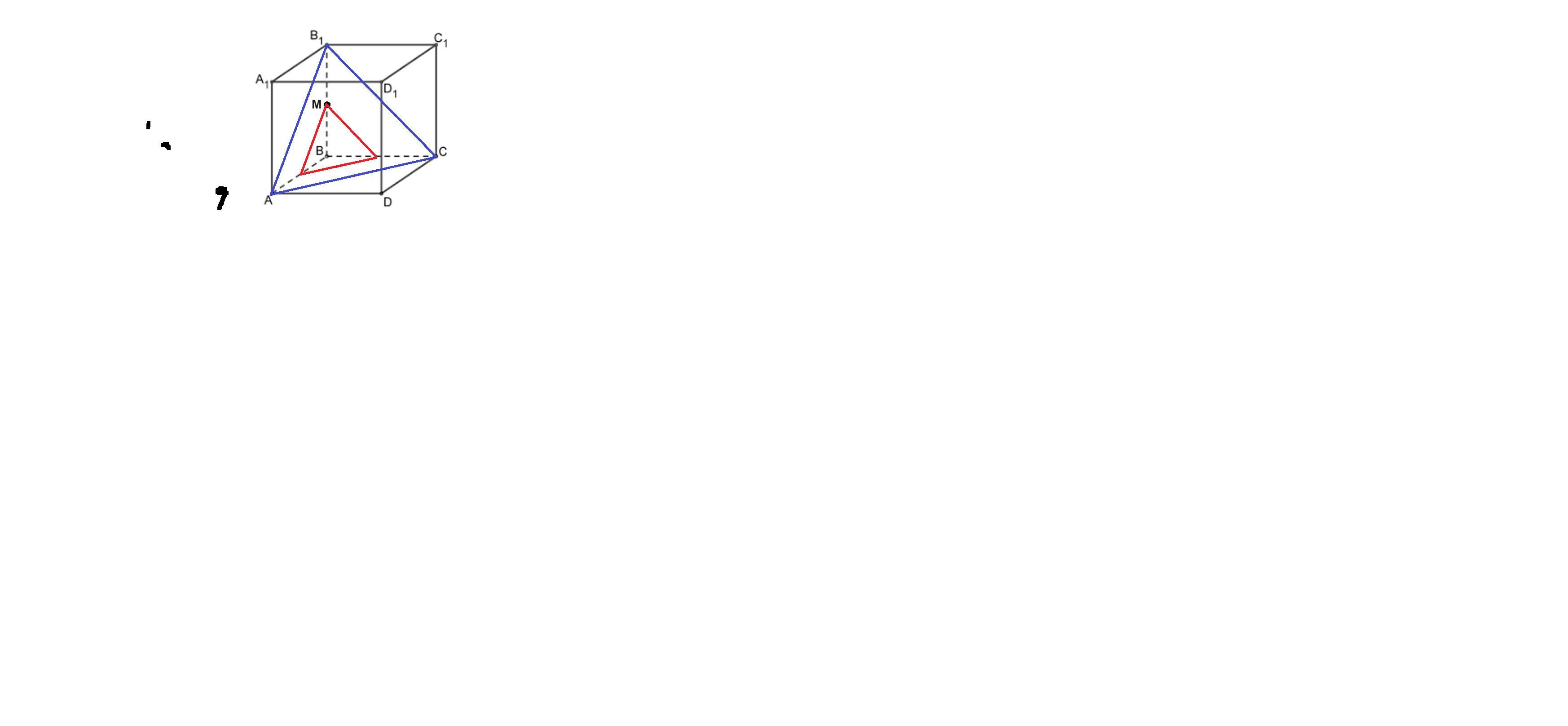
спасибо
Похожие вопросы
Предмет: Алгебра,
автор: akkauntovicakkaunt17
Предмет: Математика,
автор: wertisserafim
Предмет: Английский язык,
автор: szaporojskaya10
Предмет: Алгебра,
автор: lamezako
Предмет: История,
автор: zhaniia98