Предмет: Геометрия,
автор: picturestiktok240
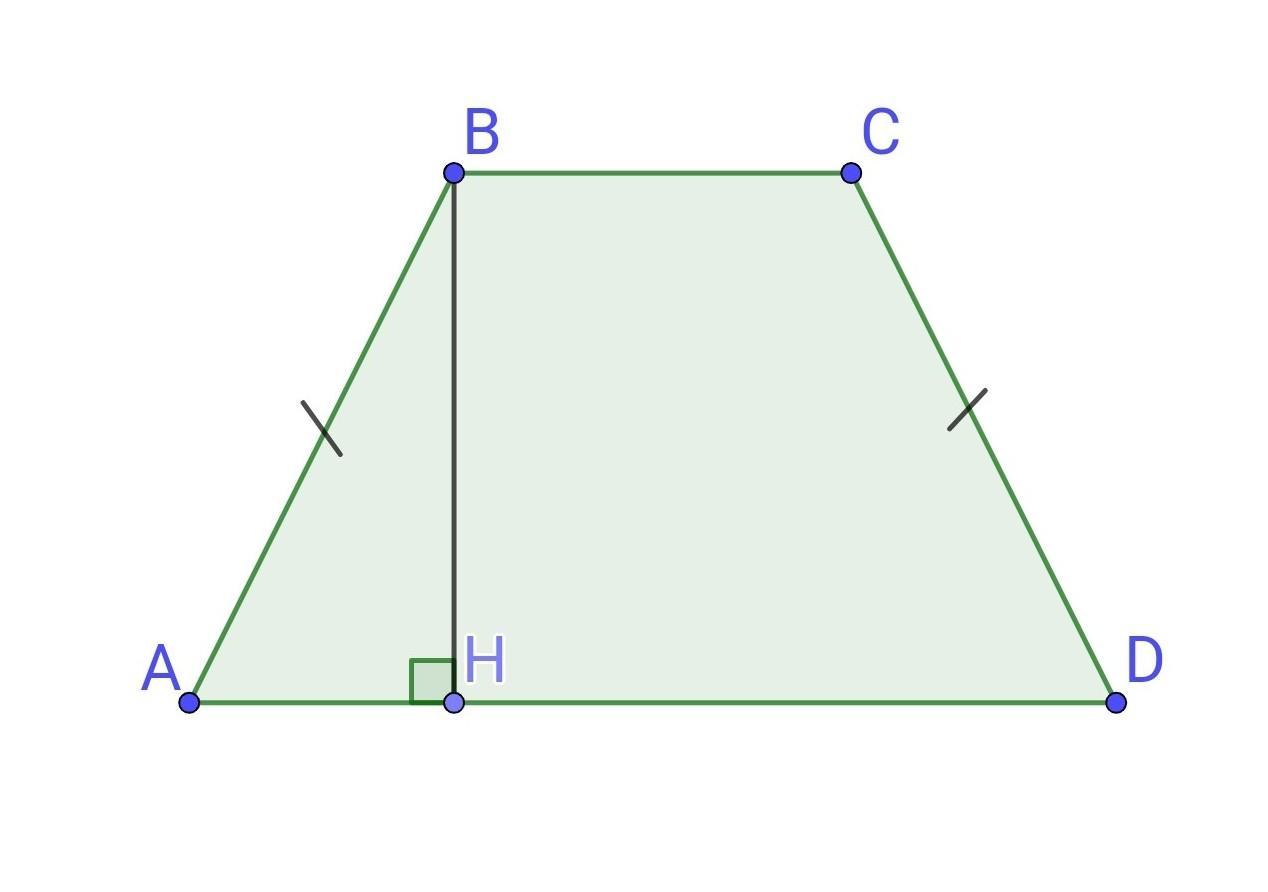
Дано: ABCD — трапеція, АВ = CD, АВ більша за ВН у 2 рази. Знайти: ∠A, ∠B, ∠C, ∠D.
Ответы
Автор ответа:
3
Ответ:
Кути трапеції дорівнюють 30°, 150°, 30°, 150°.
Объяснение:
Дано: ABCD — трапеція, АВ = CD, АВ більша за ВН у 2 рази.
Знайти: ∠A, ∠B, ∠C, ∠D.
Розв'язання
1) ВН - висота трапеції, ВН⟂AD, отже △ABH - прямокутний (∠Н=90°).
За умовою гіпотенуза АВ більша за катет ВН у 2 рази.
- Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета, дорівнює 30°.
За властивістю катета, що дорівнює половині гіпотенузи, отримаємо:
∠А=30°.
2) ∠А + ∠В = 180° - як кути, прилеглі до бічної сторони трапеції.
Тоді:
∠В = 180° - ∠А = 180° - 30° = 150°.
3) ∠D = ∠A = 30°, ∠C = ∠B = 150° - як кути при основах рівнобічної трапеції.
Відповідь: 30°,150°,150°,30°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: kravchyshynnastia
Предмет: Другие предметы,
автор: katysha0407
Предмет: Экономика,
автор: g48944098
Предмет: Қазақ тiлi,
автор: zhako1298
Предмет: История,
автор: shim270707