Question

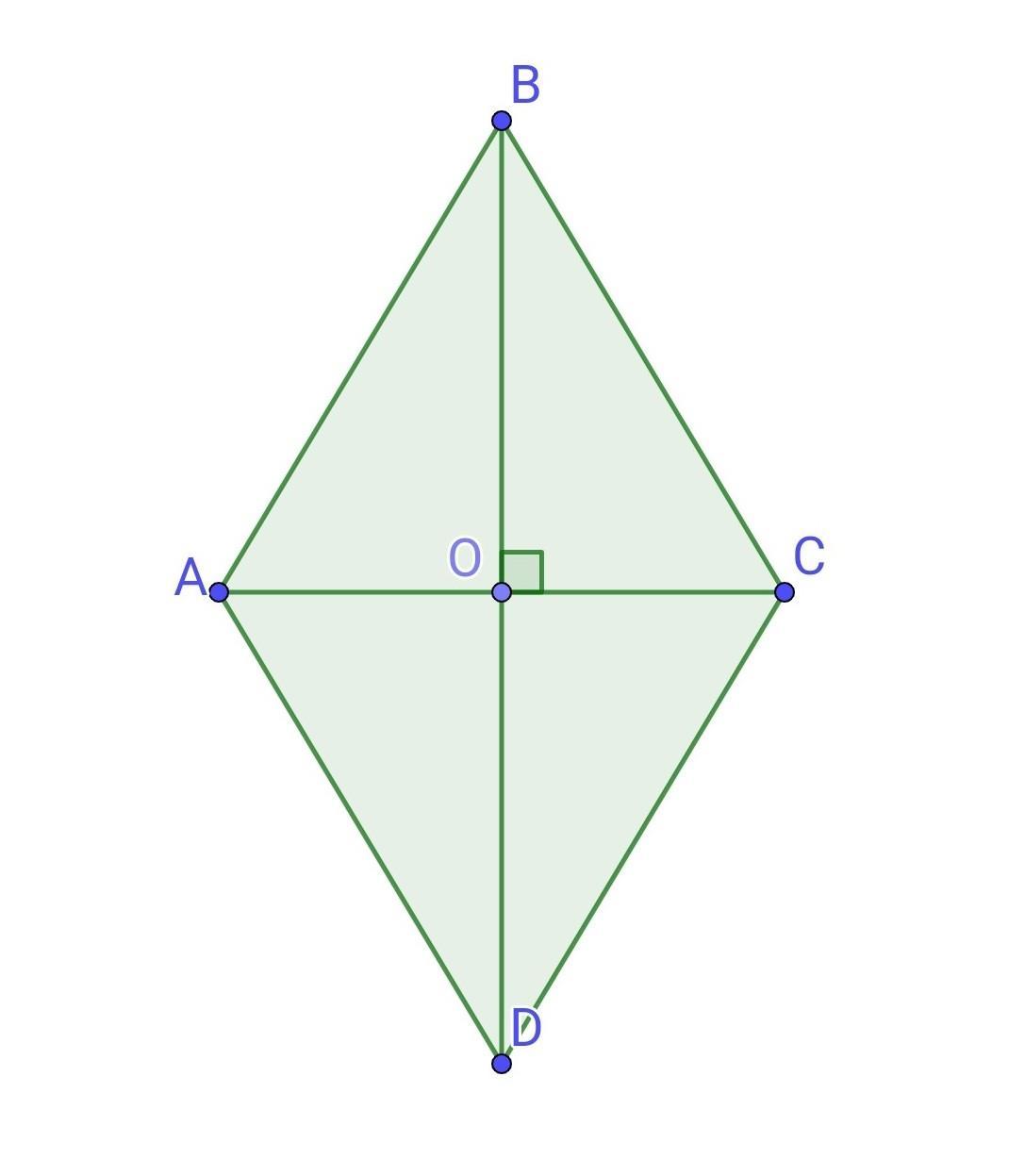
Діагоналі ромба ABCD дорівнюють 12 і 16 см, а периметр ромба становить 40 см. Знайдіть периметр трикутника AOB, де т.О - точка перетину діагоналей​

Answer 1

Ответ:

Периметр трикутника АОВ дорівнює 24 см

Объяснение:

Діагоналі ромба ABCD дорівнюють 12 і 16 см, а периметр ромба становить 40 см. Знайдіть периметр трикутника AOB, де т.О - точка перетину діагоналей.

1) Так як у ромба всі сторони рівні, то його периметр дорівнює:

Р = 4 • АВ

АВ = Р : 4 = 40 : 4 = 10 (см)

2) О - точка перетину діагоналей ромба.

За властивістю діагоналей ромба маємо:

AO = OC = ½ • AC = ½ • 12 = 6 (см)

BO = OD = ½ • BD = ½ • 16 = 8 (см)

3) Знайдемо периметр трикутника АОВ як суму всіх його сторін:

Р(АОВ) = АВ + ВО + АО = 10 + 8 + 6 = 24 (см)

Отже, периметр трикутника АОВ дорівнює 24 см.

#SPJ1