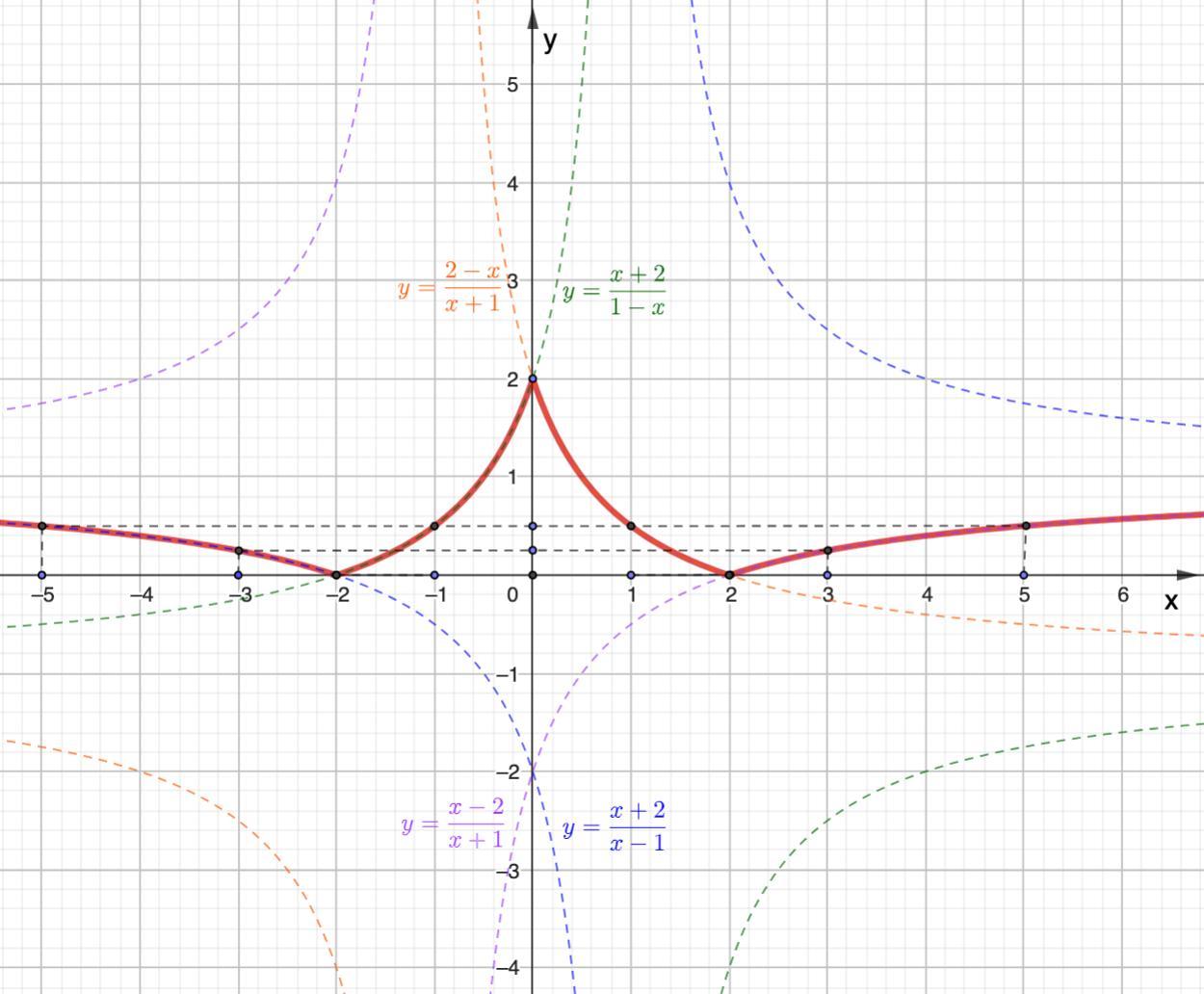
Постройте график функции и поэтапно разпишите как вы это сделали
y = |(|x| - 2)/(|x| + 1)|
Ответы
Ответ:
График построен.
Объяснение:
Построить график:
- Раскрытие модуля:
Раскроем внутренний модуль:
1) Если x ≥ 0: 2) Если x < 0:
Раскроем внешний модуль.
1) , x ≥ 0
Подмодульное выражение меняет знак в точке х = 2.
Определим знаки числителя и знаменателя на полученных промежутках:
0_____2_____
х - 2 - +
х + 1 + +
Если 0 ≤ х ≤ 2: Если x > 2:
2) , x < 0
Подмодульное выражение меняет знак в точке х = -2.
Определим знаки числителя и знаменателя на полученных промежутках:
_____-2_____0
х + 2 - +
х - 1 - -
Если x ≤ -2: Если -2 < х < 0:
Получили кусочную функцию:
Найдем точки для каждой части графика:
1.
2.
3.
4.
Строим график.
Можно построить эти четыре графика, а затем выделить нужные кусочки, соответствующие данным промежуткам.
#SPJ