5) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках;
6) знайти інтервали опуклості, вгнутості та точки перегину;
7) знайти асимптоти кривої;
8) побудувати графік функції.
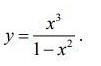
Ответы
Ответ:
График построен.
Объяснение:
Исследовать функцию и построить график:
Исследуем функцию сначала.
1. Область определения функции.
1 - х² ≠ 0 ⇒ (1 - х)(1 + х) ≠ 0
х ≠ 1; х ≠ -1
D(y) = (-∞; -1) ∪ (-1; 1) ∪ (1; +∞)
2. Четность, нечетность.
- Если f(-x) = f(x), то функция четная, если f(-x) = -f(x) - нечетная.
f(-x) = -f(x) ⇒ функция нечетная.
3. Пересечение с осями.
х = 0; у = 0.
График проходит через начало координат.
4. Непрерывность функции. Точки разрыва.
Функция определена на промежутках (-∞; -1) ∪ (-1; 1) ∪ (1; +∞) и непрерывна на этих промежутках.
Исследуем точки х = ± 1
То есть, в точках х = ±1 функция терпит бесконечный разрыв.
х = ±1 - точки разрыва второго рода.
5. Интервалы монотонности. Точки экстремумов.
Найдем производную, приравняем к нулю и найдем корни.
y' = 0 ⇒ x = 0; x = -√3; x = √3
Не забываем про х = ± 1.
Отметим их на числовой оси и определим знаки производной на промежутках.
- Если "+" - функция возрастает, если "-" - функция убывает.
Функция возрастает на промежутках: [-√3; -1); (-1; 0]; [0; 1); (1; √3];
функция убывает на промежутках: (-∞; -√3]; [√3; +∞)
- Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.
⇒ x min = -√3; x max = √3
6. Выпуклость, вогнутость.
y'' = 0 ⇒ x = 0
Отметим на числовой оси точки х = 0; х = ±1 и определим знаки на промежутках:
- Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.
Функция вогнута на промежутках: (-∞; -1); [0; 1);
функция выпукла на промежутках: (-1; 0]; (1; +∞)
х перегиба = 0; у(0) = 0.
7. Асимптоты.
Вертикальные:
⇒ x = -1; x = 1 - вертикальные асимптоты.
Наклонная: у = kx + b
y = -x - наклонная асимптота.
8. Строим график.