Question

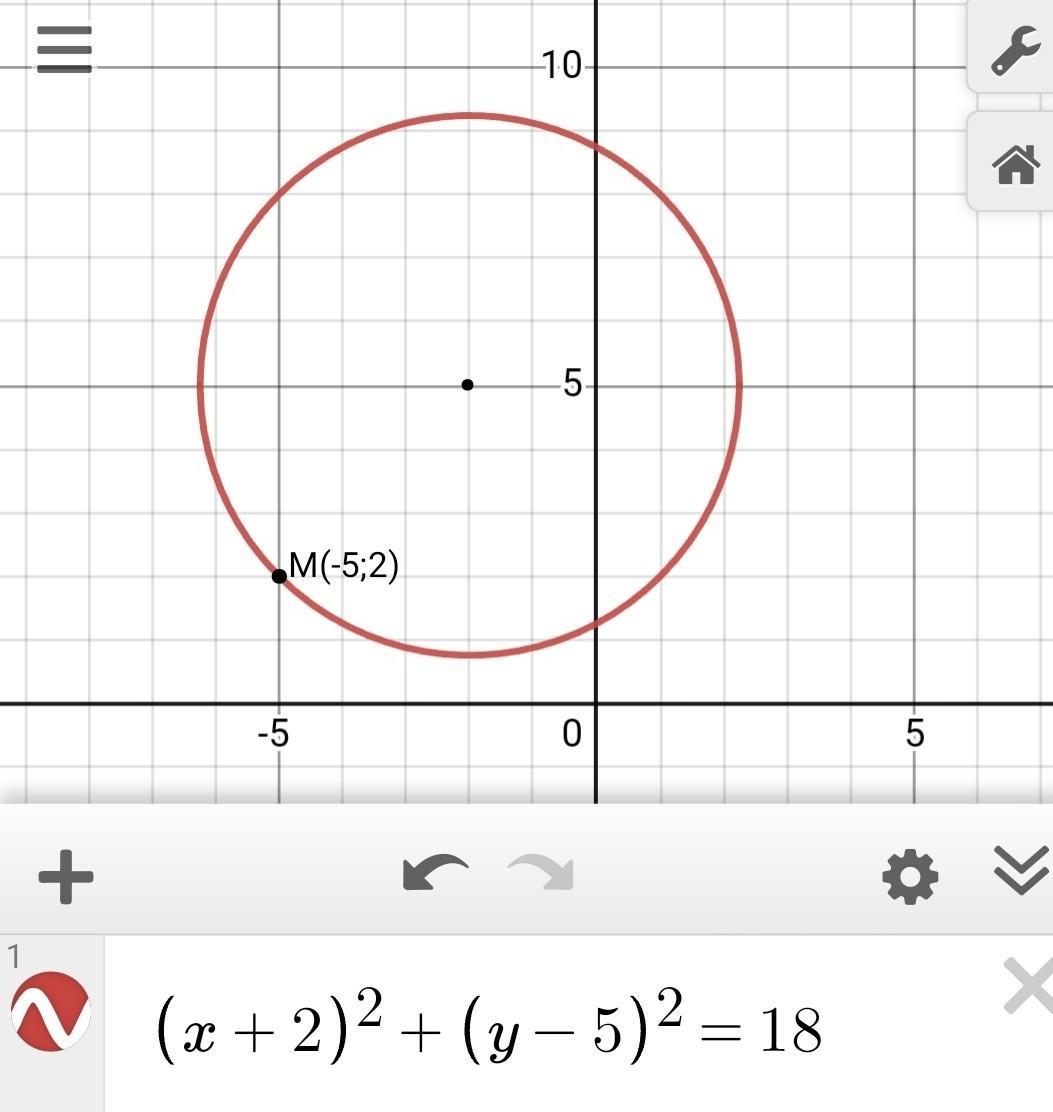
Окружность задана уравнением (x+2)^2+(y-5)^2=18. Принадлежит ли этой окружности точка M (-5;2)?

ТОЛЬКО ЧЕРТЕЖ, РЕШЕНИЕ НЕ НУЖНО
ПОМОГИТЕ ПОЖАЛУЙСТА

Answer 1

Ответ:

Точка М (-5;2) принадлежит окружности

(х+2)²+(у-5)²=18

Объяснение:

(-2;5) - центр окружности.

R=√18≈4,24.

Для решения этой задачи,нет необходимости в чертеже.

(х+2)²+(у-5)²=18

М(-5;2); абсцисса равна -5; (х=-5); ордината равна 2;(у=2)

Подставляем в уравнение х=-5; у=2. И проверяем равна ли правая и левая часть уравнения.

(-5+2)²+(2-5)²=18

(-3)²+(-3)²=18

9+9=18

18=18 (т.к. 18 равно 18, то точка М(-5;2) принадлежит окружности заданной уравнением (х+2)²+(у-5)²=18