Предмет: Алгебра,
автор: kirill2019218
Вершини трикутника
Надано вершини трикутника А(-2;5), В(0;1), С(3;-1).
Знайти: a. рівняння сторони АВ- пряма L1 ; b. рівняння висоти СН- пряма L2 .
Ответы
Автор ответа:
0
Надано вершини трикутника А(-2;5), В(0;1), С(3;-1).
Знайти: a. рівняння сторони АВ- пряма L1 ; b. рівняння висоти СН- пряма L2 .
а) Находим вектор АВ = B(0; 1) - A(-2; 5) = (2; -4).
Уравнение АВ: (х + 2)/2 = (у – 5)/(-4) или (х + 2)/1 = (у – 5)/(-2) каноническое.
-2х – 4 = у – 5,
AB: 2х + у – 1 = 0 общее.
б) Используем свойство уравнения перпендикулярной прямой.
Для прямой Ах + Ву + С1 = 0 перпендикулярная прямая имеет такое уравнение: Вх - Ау+ С2 = 0 или –Bx + Ay + C2 (из условия равенства 0 их скалярного произведения).
Находим перпендикуляр из точки С к прямой АВ: 2х + у – 1 = 0.
СН: х - 2у + С = 0. Подставим координаты точки С.
3 – 2*(-1) + С = 0, отсюда С = -3 - 2 = -5.
Уравнение СН: х - 2у - 5 = 0.
Приложения:
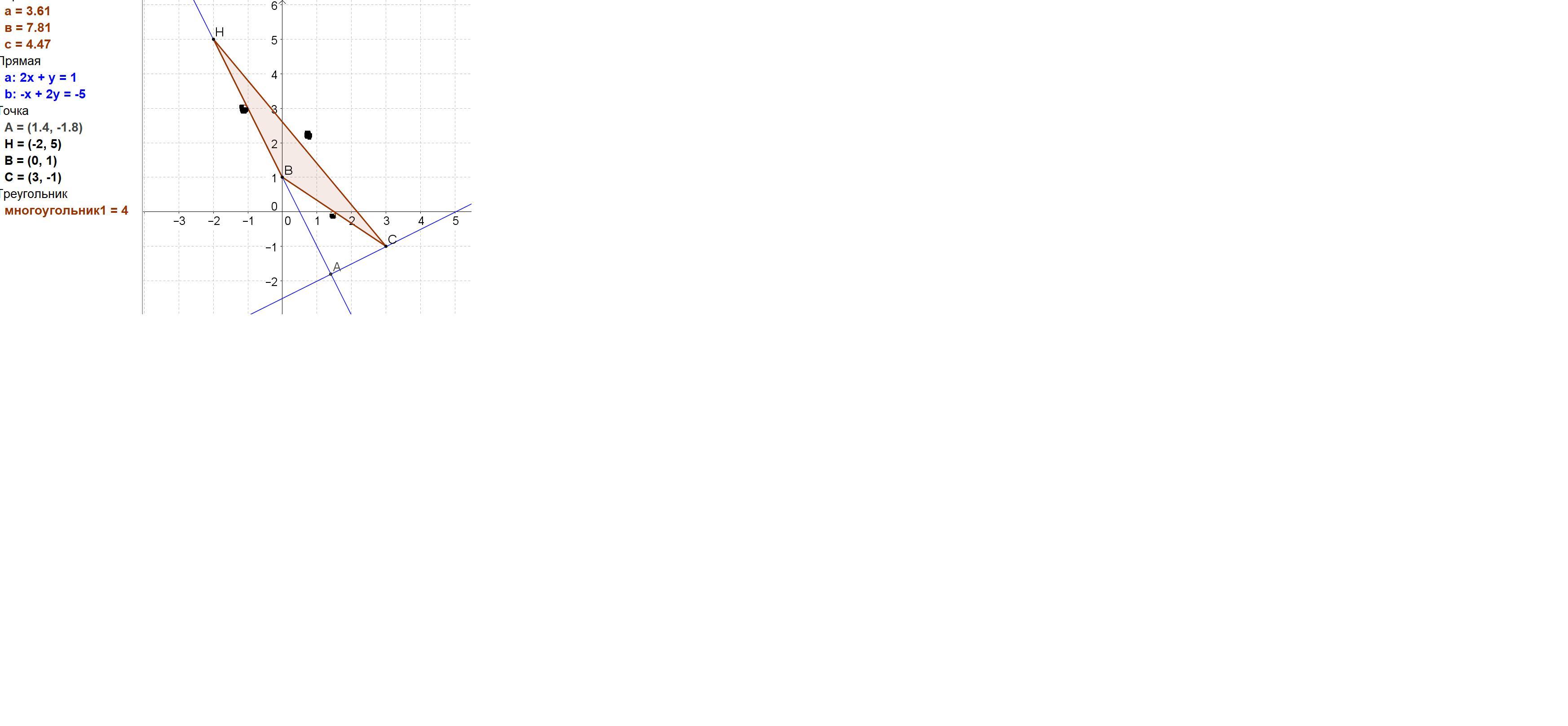
kirill2019218:
Поможете решить другую задачу в профилье? "Розв’язати систему ЛАР"
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Українська література,
автор: nikitazurawskiy
Предмет: Химия,
автор: androsova16
Предмет: Русский язык,
автор: dojdik01bekov