Предмет: Математика,
автор: ffggweryn
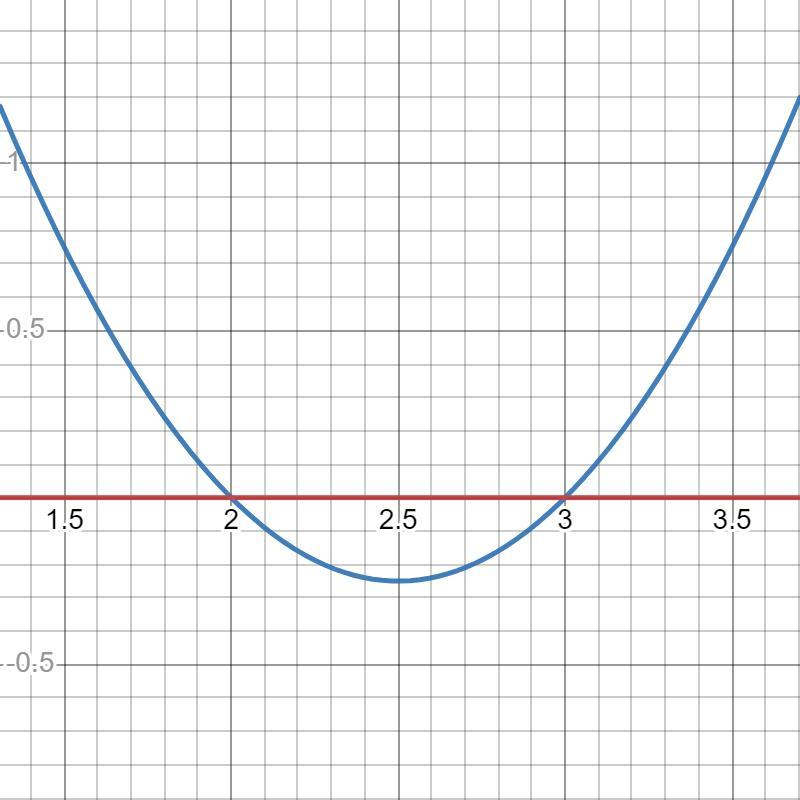
Обчисліть площу фігури, обмежену лініями 1)y=x^ 2 -5x+6, y = 0; 2)y=cos x,; y = 0; x = 2pi
Ответы
Автор ответа:
1
Покрокове пояснення:
1)
Відповідь: S=0,16667 кв. од.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: n622832
Предмет: Українська мова,
автор: basovakata590
Предмет: Українська мова,
автор: nugi66600
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: Аноним