Question

Знайти меншу діагональ правильного шестикутника, якщо більша його діагональ дорівнює 2/3 см.

Answer 1

Ответ:

Объяснение:

Дано:
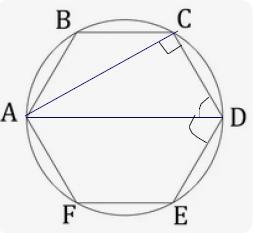
ABCDEF - правильный шестиугольник
AD = 2/3 (см)
___________
АС - ?см

1) Все углы правильного шестиугольника равны между собой
∠А = ∠В = ... = ∠D =  (n-2)*180)/n = (6 - 2)*180°/6 = 120°

2)  Вокруг правильного шестиугольника  можно описать окружность, и притом только одну.  Радиус описанной окружности является биссектрисой угла правильного шестиугольника, т.е
∠CDA = ∠EDA = 120°/2 = 60°
3) ∠ACD = 90°, т.к. он является вписанным и опирается на диаметр окружности.
Следовательно, ΔACD - прямоугольный.
АС = AD*sin∠CDA = AD * sin60° = ²/₃ * √3/2 = √3/3

AC = √3/3 (см)