Предмет: Математика,
автор: hodenly62
помогите, пожалуйста, решить замечательные пределы
Приложения:
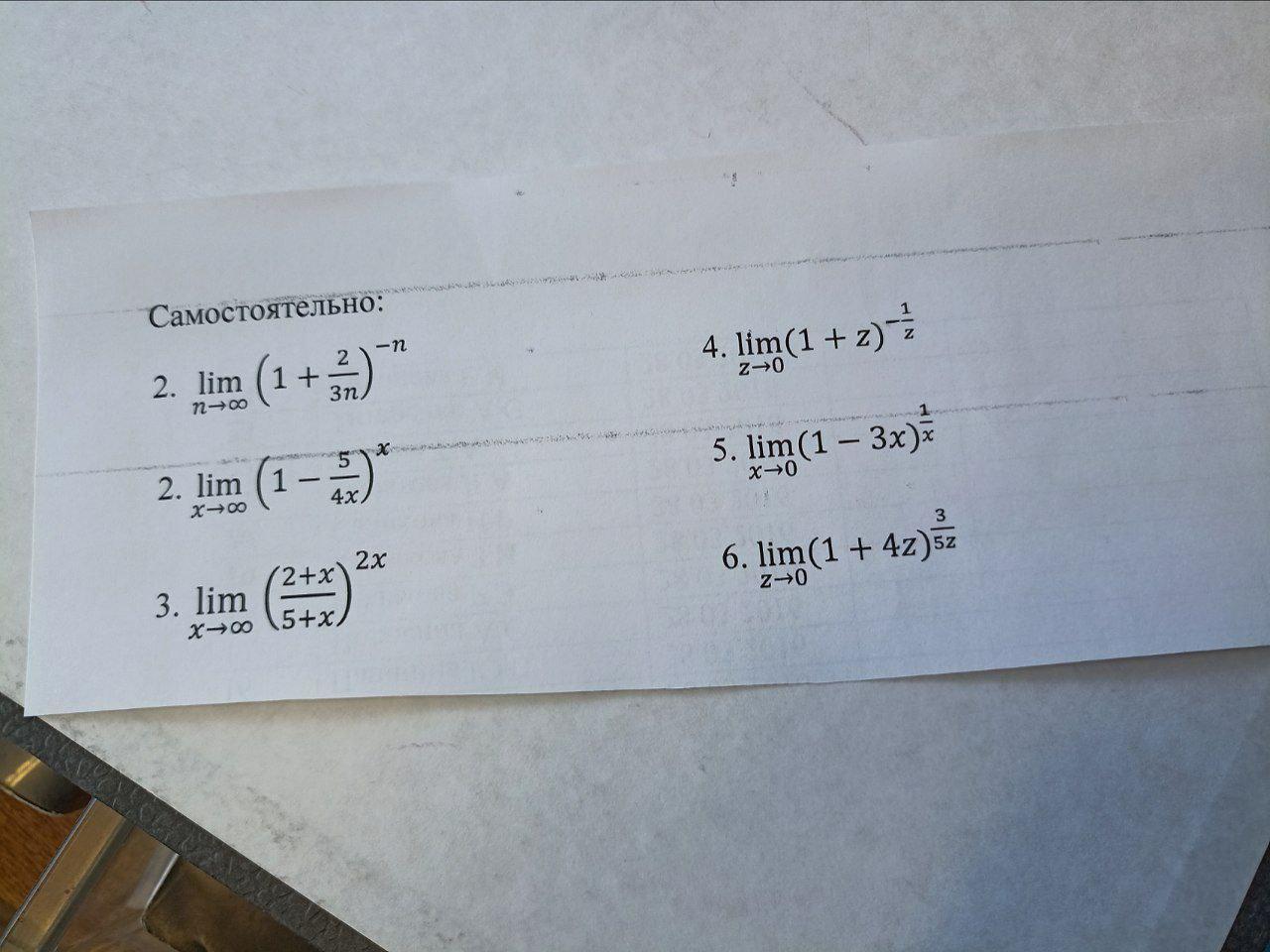
Ответы
Автор ответа:
0
Ответ:
Второй замечательный предел :
Приложения:

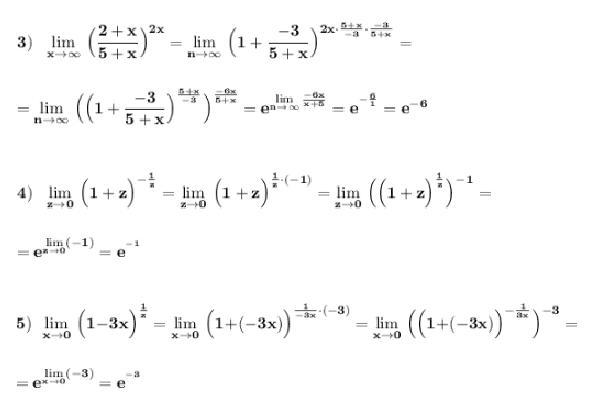
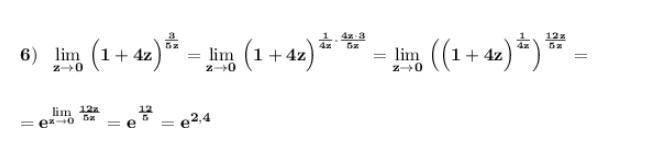
Похожие вопросы
Предмет: Английский язык,
автор: lera2203201200
Предмет: Алгебра,
автор: stasovskaana151
Предмет: Другие предметы,
автор: msemykopenko1
Предмет: Русский язык,
автор: ULTRANASOS
Предмет: Биология,
автор: Аноним