Question

помоги пожалуйста прошу ​

Answer 1

Ответ:

Установили соответствие:

1 → В;   2 → Д;   3 → Б;   4 → А.

Пошаговое объяснение:

Установите соответствие между уравнением или неравенством (1-4) и количеством его целых решений (А-Д).

Решим данные уравнения и неравенства и определим количество корней.

1.  

$\displaystyle \bf 4^x-3\cdot 2^x=4\\\\2^{2x}-3\cdot2^x-4=0$

Замена переменной:

$\displaystyle \bf 2^x=t;\;\;\;t > 0$

$\displaystyle \bf t^2-3t-4=0$

По теореме Виета:

$\displaystyle \bf t_1 =4;\;\;\;\;\;t_2=-1$

$t_2$ - не подходит, так как t > 0

⇒ уравнение имеет одно целое решение.

2.

$\displaystyle \bf 5^{2x-x^2}\geq \frac{1}{125} \\\\5^{2x-x^2}\geq 5^{-3}\\\\2x-x^2\geq -3\\\\x^2-2x-3\leq 0$

Найдем корни уравнения по теореме Виета:

$\displaystyle \bf x^2-2x-3=0\\\\x_1 =3;\;\;\;\;\;x_2=-1$

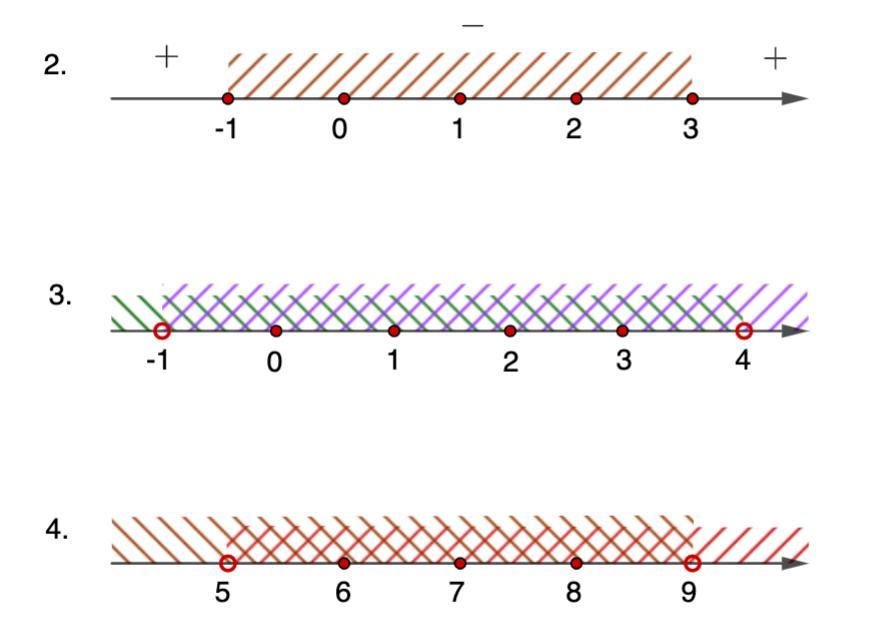
Отметим корни на числовой оси, определим знаки на промежутках.

Решением неравенства будет промежуток

-1 ≤ х ≤ 3

⇒ неравенство имеет пять целых решение {-1; 0; 1; 2; 3}

3.

$\displaystyle \bf lg(4-x)+lg(x+1)=lg(4+3x-x^2)$

ОДЗ:

1) 4 - x > 0   ⇒   x < 4

2) x + 1 > 0   ⇒   x > -1

3) 4 + 3x - x² > 0   или   x² - 3x - 4 < 0  

x₁ = 4;     x₂ = -1   ⇒   -1 < x < 4

⇒ x ∈ (-1; 4)

• Свойство логарифмов:

     logₐb + logₐc = logₐbc

$\displaystyle \bf lg(4-x)(x+1)=lg(4+3x-x^2)\\\\4x+4-x^2-x=4+3x-x^2\\\\0 = 0$

Учитывая ОДЗ:  x ∈ (-1; 4), получим четыре целых решения {0; 1; 2; 3}

4.

$\displaystyle \bf log_{0,5}(9-x) > -2$

ОДЗ:

9 - х > 0   ⇒   x < 9

x ∈ (-∞; 9)

$\displaystyle \bf log_{0,5}(9-x) > log_{0,5}0,5^{-2}\\\\ log_{0,5}(9-x) > log_{0,5}4\\\\9-x < 4\\\\x > 5$

Учитывая ОДЗ, получим:  5 < x < 9

Неравенство имеет три целых решения {6; 7; 8}