Предмет: Алгебра,
автор: egorthreeaxe
Решить систему уравнений способом подстановки
Приложения:
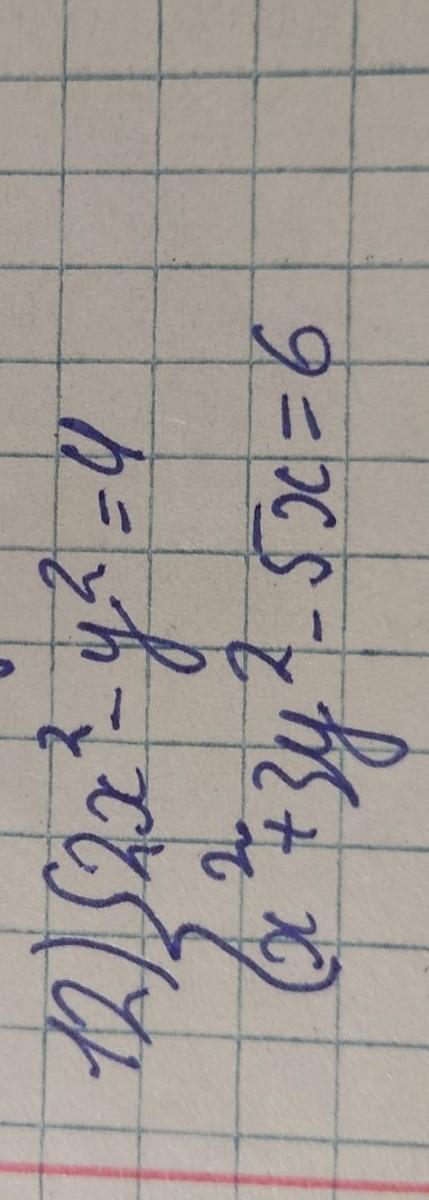
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: galchenkoanita28
Предмет: Математика,
автор: azidkova682
Предмет: Українська мова,
автор: kuzmenkoanastasia777
Предмет: Қазақ тiлi,
автор: termek84
Предмет: Математика,
автор: Tour1312