Предмет: Математика,
автор: mikrob4928
Доказать тождество (задание на фото)
Приложения:
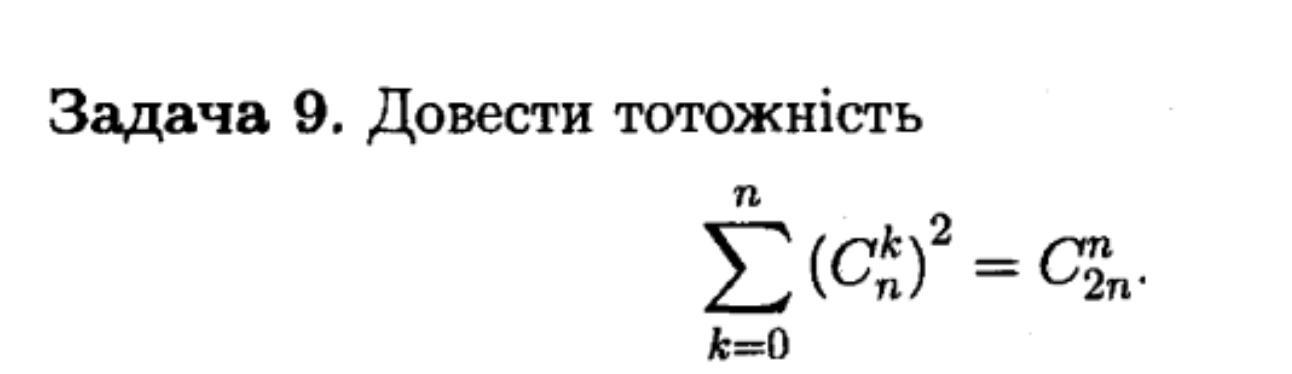
Ответы
Автор ответа:
2
Бином Ньютона:
Следовательно:
Коэффициенты при члене xⁿ равны:
Очевидно, что:
Тогда:
QED
vkook777:
Вау, превосходный ответ!
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Геометрия,
автор: Sophifiti
Предмет: Математика,
автор: dragazgms
Предмет: Английский язык,
автор: fadeeva110
Предмет: Алгебра,
автор: limityg23