ГЕОМЕТРИЯ ПОЖАЛУЙСТА СРОЧНО

Ответы
Воспользуемся
теоремой синусов
:
Стороны треугольника пропорциональны синусам противолежащих углов.
В нашем случае:
Подставим известные значения (OP, PR, sin ∠O).
(∠POR для удобства будем писать как ∠О)
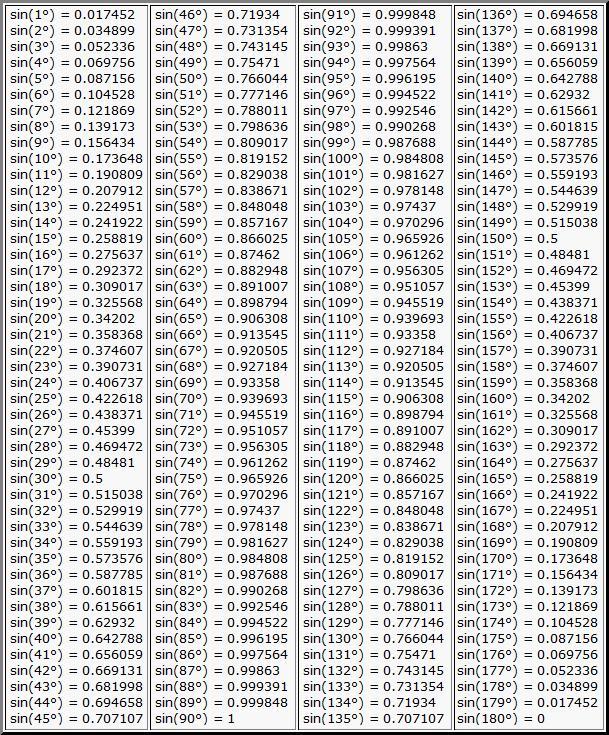
Синус ∠О мы должны посмотреть в таблице значений синусов углов (см. фото). Он равен примерно 0.866
Для удобства примем sin R за x.
Мы знаем, что в равных дробях произведение числителя одной дроби со знаменателем второй дроби равно произведению знаменателя первой дроби с числителем второй дроби ("перекрёстное правило"). Это значит, что:
√3 · х = √2 · 0.866
Решим полученное уравнение:
√3 · х ≈ 1.225
х ≈ 1.225 : √3 ≈ 0.707 (sin R)
А чтобы найти ∠R, необходимо в таблице найти синус, максимально приближенный к тому, что у нас получился (0.707).
Получаем, что наш угол равен 45°.
(в подобных задачах возможны погрешности)
Ответ:
∠R = 45°