Предмет: Математика,
автор: yarandinaalina
Дослідити функцію на неперервність. Додаю фото завдання ( Варіант 1 )
Приложения:

Ответы
Автор ответа:
0
Ответ:
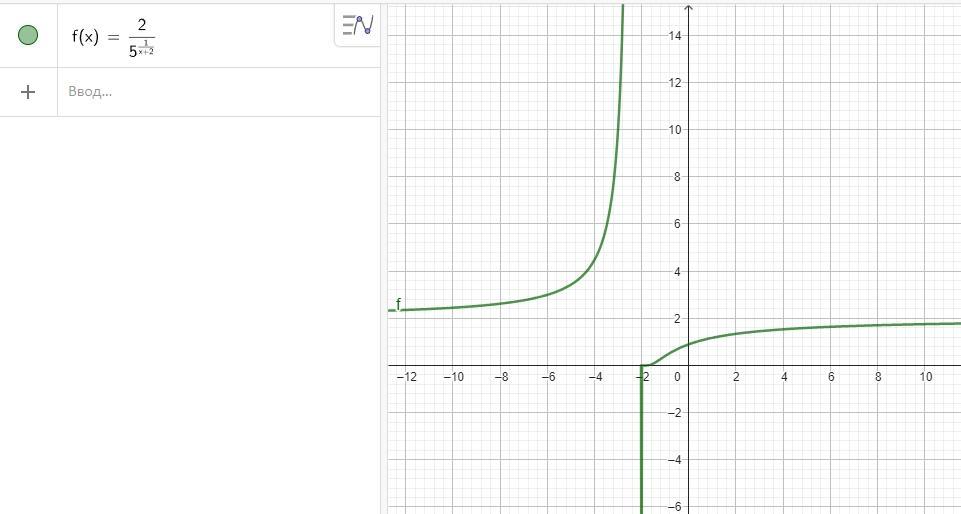
точка разрыва первого рода х₀ = (-2)
Пошаговое объяснение:
Точка разрыва х₀ = (-2)
посмотрим, как ведет себя функция при х → (-2) слева и справа
предел слева
Аналогично считаем предел справа
опускаю предыдущие вычисления, они такие же как выше
в конце получим
и, поскольку (х+2) >0
получаем
Если в точке a существуют конечные, но не равные между собой пределы функции f(x) справа и слева, то a называется точкой разрыва первого рода.
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: oal770046
Предмет: Химия,
автор: eakalu17
Предмет: Информатика,
автор: aabrvanec
Предмет: Астрономия,
автор: Аноним
Предмет: Информатика,
автор: zerozz623