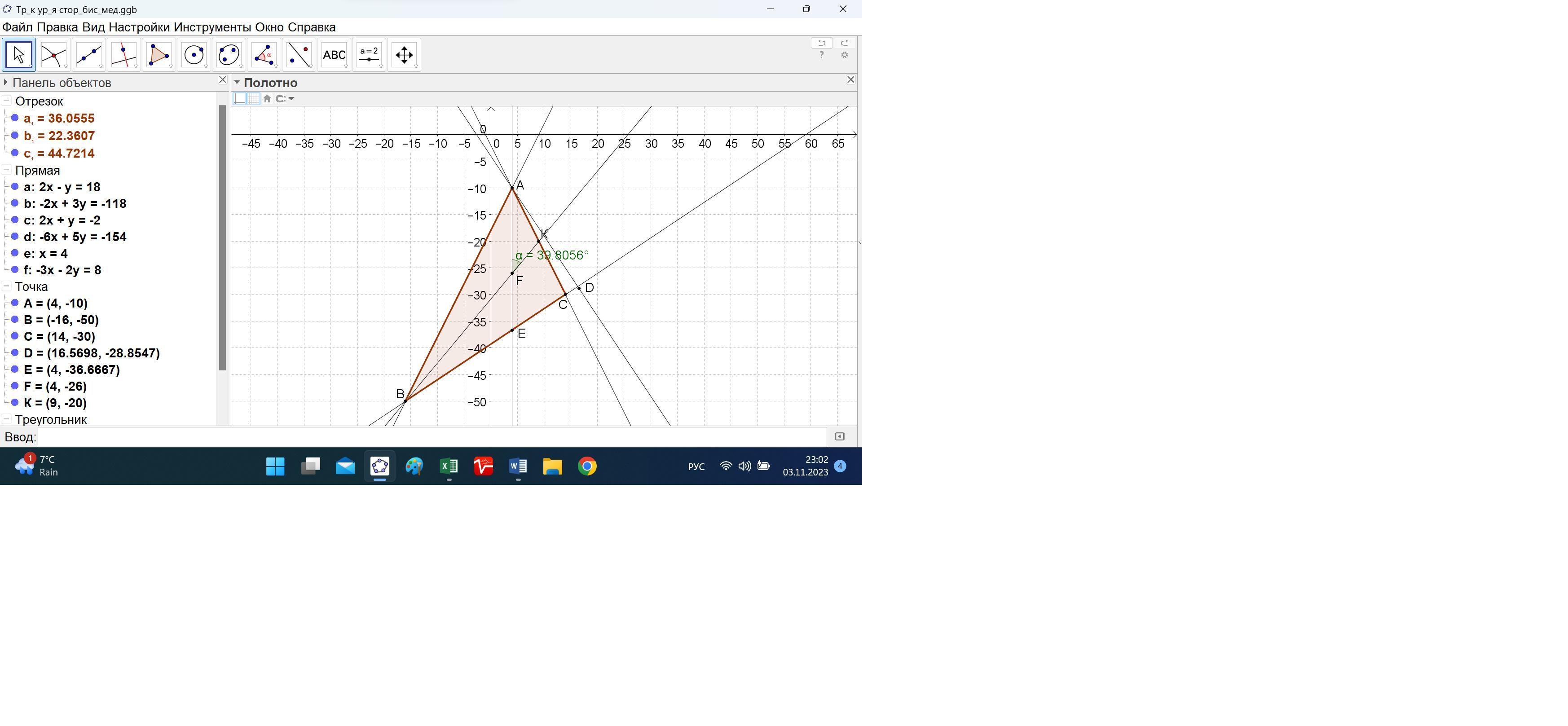
ЗТрикутник АВС задано координатами вершин А(4;-10,). B(-16;-50) С(14: -30,). Знайти рівняння сторони АВ, бісектриси АЕ, медіани ВК, висоти AD та її довжину, площу трикутника і кут між бісектрисою та медіаною.
Треугольник ABC задан координатами вершин A(4;-10,). B(-16;-50) С(14: -30,). Найдите уравнение стороны АВ, биссектрисы АЕ, медианы ВК, высоты AD и ее длины, площади треугольника и угла между биссектрисой и медианой.
Ответы
Треугольник ABC задан координатами вершин A(4;-10,). B(-16;-50) С(14: -30,). Найдите :
1) уравнение стороны АВ,
2) биссектрисы АЕ,
3) медианы ВК,
4) высоты AD и ее длины,
5) площадь треугольника,
6) угол между биссектрисой AE и медианой BK.
1) Вектор АВ = (-16-4; -50-(-10)) = (-20; -40).
Уравнение АВ: (х – 4)/(-20) = (у + 10)/(-40),
Или (х – 4)/1 = (у + 10)/2 каноническое.
2х – 8 = у + 10, 2х – у – 18 = 0 общее.
2) Используем уравнение прямой AВ: 2х – у – 18 = 0.
Находим уравнение прямой AС.
Вектор AС = (14-4; -30-(-10)) = (10; -20).
Уравнение AС: (х - 4)/(10) = (у + 10)/(-20),
Или (х - 4)/1 = (у + 10)/(-2) каноническое.
-2х + 8 = у + 10, 2х + у + 2 = 0 общее.
Теперь используем формулу биссектрисы.
(A1x + B1y + C1)/√(A1² + B1²) = ±(A2x + B2y + C2)/√(A2² + B2²)
Но сначала находим знаменатель.
√(A1² + B1²) = √(2² + (-1)²) = √5,
√(A2² + B2²) = √(2² + 1²) = √5.
Составляем уравнение: (2х – у – 18)/ √5 = ±(2х + у + 2)/ √5.
Получаем первое уравнение: 2х – у – 18 = 2х + у + 2.
2у = -20 или у = -20/2 = -10.
Получаем второе уравнение: 2х – у – 18 = -(2х + у + 2).
4х = 16 или х = 16/4 = 4.
Но первое уравнение даёт биссектрису внешнего угла, поэтому оставляем уравнение АЕ: х = 4.
3) Находим координаты точки К как середины отрезка АС.
К = (A(4;-10) + С(14; -30)/2 = (9; -20).
Определяем вектор ВК:
К(9; -20) - B(-16; -50) = (25; 30).
Теперь составляем уравнение медианы ВК.
ВК: (х + 16)/25 = (у + 50)/30 или (х + 16)/5 = (у + 50)/6 каноническое.
6х + 96 = 5у + 250,
ВК: 6х – 5у – 154 = 0 общее.
4) Высота AD - это перпендикуляр к стороне ВС.
Находим уравнение ВС.
Определяем вектор ВС по точкам B(-16; -50) С(14; -30).
ВС = С(14; -30) - B(-16; -50) = (30; 20).
Теперь составляем уравнение стороны ВС.
ВС: (х + 16)/30 = (у + 50)/20 или (х + 16)/3 = (у + 50)/2 каноническое.
2х + 32 = 3у + 150,
2х – 3у – 118 = 0 общее.
Уравнение стороны ВС в общем виде Ах + Ву + С = 0.
Для перпендикулярной прямой коэффициенты А и В меняются на (-В) и А или В и (-А).
Уравнение высоты из точки А получаем 3х + 2у + С = 0.
Для определения слагаемого С подставим координаты точки A(4;-10).
3*4 + 2*(-10) + С = 0, отсюда С = 20 - 12 = 8.
Получаем AD: 3х + 2у + 8 = 0.
5) Площадь треугольника равна половине модуля векторного произведения векторов ВА и ВС.
Вектор ВА равен –АВ = -(-20; -40) = (20; 40), его модуль равен √(20² + 40²) = √(400 + 1600) = √2000 = 20√5.
Вектор ВС уже определён и равен (30; 20).
Модуль равен √(30² + 20²) = √(900 + 400) = √1300 = 10√13.
Находим векторное произведение ВА и ВС с применением схемы Саррюса.
BAxBC = i j k| i j
20 40 0| 20 40
30 20 0| 30 20 = 0i + 0j + 400k – 0j – 0i -1200k.
BAxBC = (0; 0; -800).
S(ABC) = (1/2)√(0² + 0² + (-800)²) = (1/2)*800 = 400 кв. ед.
6) Биссектриса АЕ: х = 4, медиана ВК: 6х – 5у – 154 = 0.
Угловой коэффициент ВК найдём из уравнения ВК в виде с угловым коэффициентом.
ВК: у = (6/5)х – (154/5).
Угол наклона ВК к оси Ох равен arctg(6/5) = 0,87606 радиан или 50,19443 градуса.
Так как прямая х = 4 это вертикальная прямая с углом 90 градусов, то искомый угол между биссектрисой АЕ и медианой ВК равен 90 – 50,19443 = 39,80557 градуса.