Пожалуйста помогите (2 часть)
1,3,4 часть задания в профиле
за каждое уравнение 9 балов
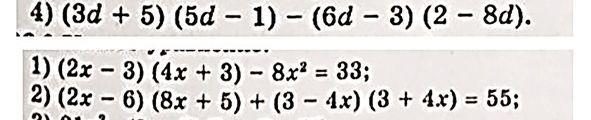
Ответы
Ответ:
Конечно, упростим уравнения без нахождения конкретных значений переменных:
1) \((3d + 5)(5d - 1) - (6d - (2 - 8d))\)
Раскроем скобки:
\(15d^2 - 3d + 25d - 5 - 6d - 2 + 8d\)
Упростим:
\(15d^2 + 20d - 7\)
\((2x - 3)(4x + 3) - 8x^2 = 33\)
Раскроем скобки:
\(8x^2 + 6x - 12x - 9 - 8x^2 = 33\)
Упростим:
\(6x - 12x - 9 = 33\)
(-6x - 9 = 33
2). \((2x - 6)(8x + 5) + (3 - 4x)(3 + 4x) = 55\)
Раскроем скобки:
\(16x^2 + 10x - 48x - 30 + 9 - 12x^2 = 55\)
Упростим:
\(4x^2 - 38x - 21 = 55\)
4)
Давайте упростим данное выражение:
Сначала умножим каждую пару скобок:
1. (3d + 5)(5d - 1) = 15d^2 + 5d - 3d - 5
2. (6d - 3)(2 - 8d) = 12d - 48d^2 - 18 + 24d
Теперь вычтем второе выражение из первого:
(15d^2 + 5d - 3d - 5) - (12d - 48d^2 - 18 + 24d)
Распределите знак минус во втором выражении:
15d^2 + 5d - 3d - 5 - 12d + 48d^2 + 18 - 24d
Теперь объедините подобные члены:
(15d^2 + 48d^2) + (5d - 3d - 24d) + (-5 + 18)
Это даст вам:
63d^2 - 22d + 13
Итак, упрощенное выражение равно 63d^2 - 22d + 13.