2. Найдите множество точек координатной плоскости, которое задано системой неравенств: y2x-4 ||x+1 + y+2|2<4
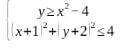
Ответы
Ответ:
Давайте розв'яжемо систему нерівностей та знайдемо множину точок на координатній площині, яка задана нерівністю:
y²x - 4 ||x + 1 + y + 2||² < 4
1. Розглянемо внутрішній модуль ||x + 1 + y + 2||²:
x + 1 + y + 2 = x + y + 3
2. Тепер ми маємо:
y²x - 4(x + y + 3) < 4
3. Розглянемо нерівність детальніше:
y²x - 4x - 4y - 12 < 4
4. Перенесемо всі члени на одну сторону нерівності:
y²x - 4x - 4y - 12 - 4 < 0
5. Спростимо:
y²x - 4x - 4y - 16 < 0
6. Тепер ми можемо розв'язати цю нерівність. Простіше всього зробити це графічно, або використовуючи область визначення y, x, наприклад, розглянувши весь різницю:
-∞ < x < ∞
-∞ < y < ∞
Ця нерівність задає всю координатну площину. Тобто, множина точок, що задовольняють цій нерівності, - це увесь простір (усі точки на координатній площині).
Объяснение: