Предмет: Алгебра,
автор: evaketb123
СРОЧНО ПОЖАЛУЙСТА ДАМ 20 БАЛЛОВ
Приложения:
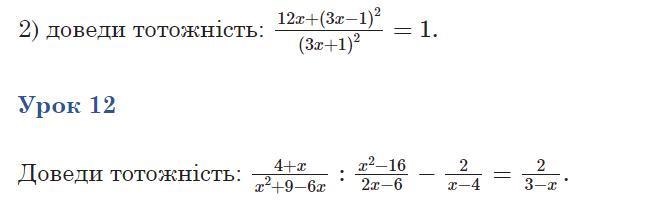

Ответы
Автор ответа:
0
Объяснение:
2)
Урок 12.
1)
2)
Ответ: х=17.
Похожие вопросы
Предмет: Русский язык,
автор: acon5068
Предмет: Алгебра,
автор: Nikita123144
Предмет: Физика,
автор: annushka2791998
Предмет: Литература,
автор: Аноним