Сіткою довжиною 200 м потрібно обгородити прилягаючу до будинку прямокутну ділянку найбільшої площі. Знайти розміри прямокутної ділянки
Ответы
Ответ:
Найбільша площа ділянки дорівнює 2500 м²
Пошаговое объяснение:
Сіткою довжиною 200 м потрібно обгородити прилягаючу до будинку прямокутну ділянку найбільшої площі. Знайти розміри прямокутної ділянки.
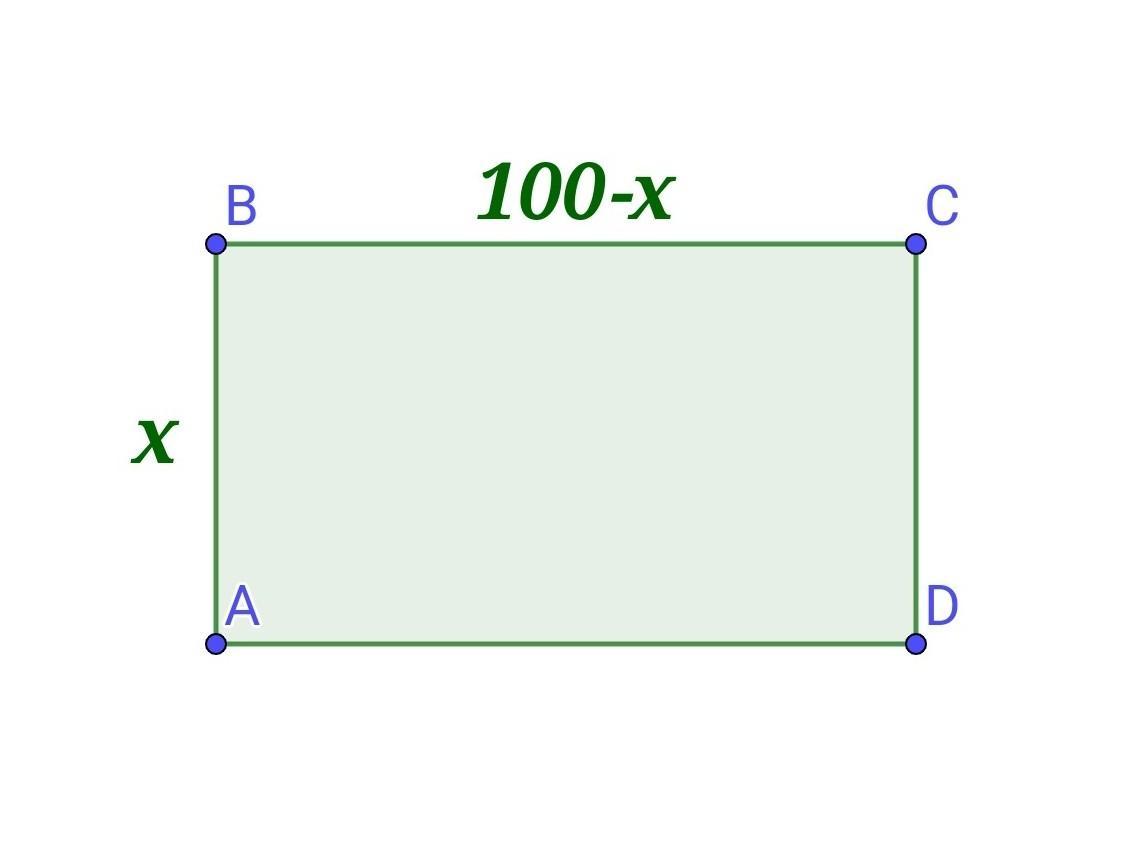
Ділянка має форму прямокутника ABCD, зі стороною АВ = х (м).
Р(ABCD) = 200 м
P(ABCD) = 2(AB+BC)
2(AB+BC) = 200
AB + BC = 100.
Отже, ВС = 100 - АВ = 100 - х (м).
Оскільки довжина кожної сторони є дотатним числом, то 0<х<100.
Площа прямокутника:
S(ABCD)=AB•BC=x•(100-x)=100x-x²
Розглянемо функцію S(x)=100x-x².
Це квадратична функція, її графік - парабола, вітки якої напрямлені вниз.
Найбільшого значення ця функція набуває у вершини параболи, тобто при
Це значення належить заданому інтервалу (0;100), отже на цьому проміжку функція набуває найбільшого значення при х=50.
S(50) = 100 • 50 - 50² = 5000 - 2500 = 2500.
Число 2500 є найбільшезначення функції S(x) = 100x-x², тому найбільша площа ділянки дорівнює 2500м².
#SPJ1