1. Точка 0- центр правильного четырехугольника ABCD, сторона которого равна 20. Найдите радиус описанной около него окружности.
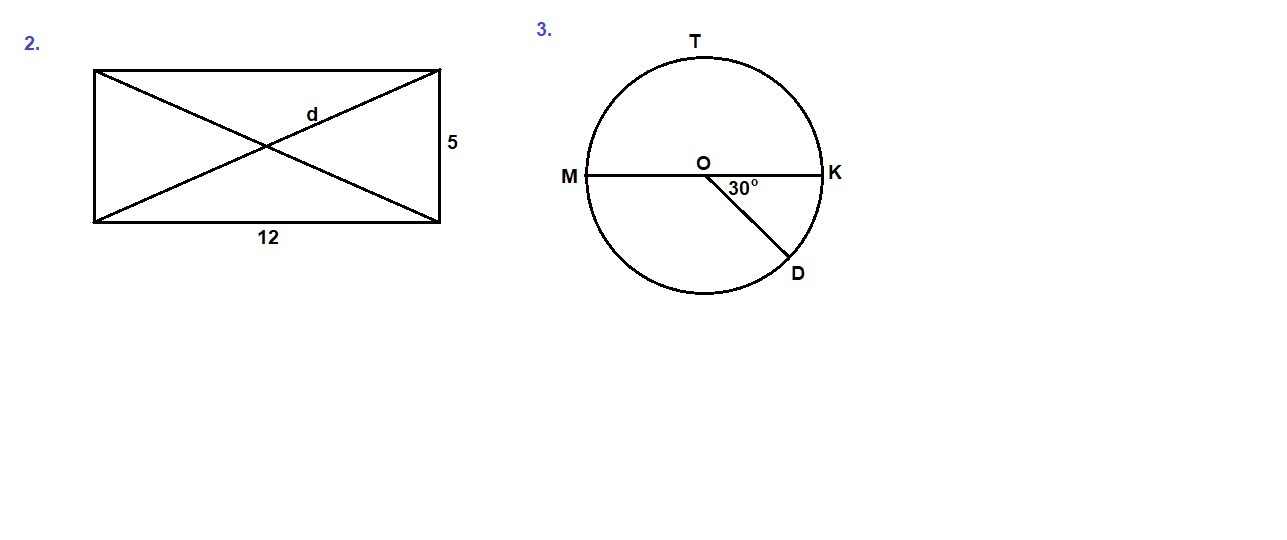
2. Найдите длиннц=у окружности, описанной около прямоугольника со сторонами 12 см и 5 см.
3. В окружности с центром 0 и радиусом 5 см проведены диаметр МК и радиус OD. Найдите длины дуг, на которые делят окружность точки М, К и D, если /_ KOD= 30 градусов.
4. Около правильного шестиугольника со стороной 12 см описана окружность. Найдите площадь кругогого сектора, соответствующему центральному угу шестиугольника
Ответы
1. Правильный четырехугольник - квадрат. Радиус описанной около квадрата окружности равен половине диагонали.
Если а - сторона квадрата, d - диагональ и R - радиус описанной окружности, то
d = a√2 = 20√2.
R = d/2 = 10√2
2. Центр окружности, описанной около прямоугольника, лежит в точке пересечения его диагоналей. Диагонали прямоугольника равны и являются диаметрами окружности.
По теореме Пифагора:
d = √(12² + 5²) = √(144 + 25) = √169 = 13 см
Длина окружности:
C = πd = 13π см
3. ∠KOD = 30° - центральный угол, значит и градусная мера соответствующей ему дуги тоже 30°.
∪ DK = 30°
∠МОК = 180° ⇒ ∪ MTK = 180°,
∪ MD = 360° - 180° - 30° = 150°
Длина дуги находится по формуле:
С = 2πR · α / 360°
С_dk = 2π · 5 · 30° / 360° = 5π/6 см
C_mtk = 2π · 5 · 180° / 360° = 5π см
C_md = 2π · 5 · 150° / 360° = 25π/6 см
4. Радиус окружности, описанной около правильного шестиугольника, равен стороне шестиугольника:
R = a = 12 см
Центральный угол правильного шестиугольника:
α = 360° / 6 = 60°
Площадь кругового сектора:
S = πR² · α / 360°
S = π · 144 · 60° / 360° = 24π см²