Срочно!! Потрібна допомога!
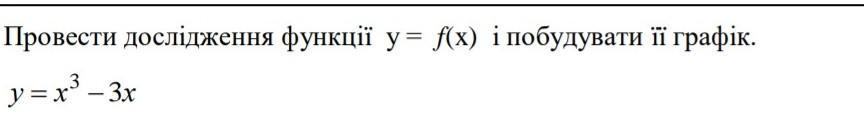
Ответы
Ответ:
в объяснении
Пошаговое объяснение:
y = x³ - 3x
1) Область допустимых значений.
вся числовая ось.
D(y)={x∈R}
2) Область значений функции
вся числовая ось.
E(y)={y∈R}
3) нули функции
x³ - 3x = х(х² - 3)
х(х² - 3) = 0 ⇒
4) Пересечение с осями
ось ОХ (y=0)
ось OY (x=0) y = 0-3*0=0 y₁ = 0
5) Точки разрыва.
функция непрерывна на всей области определения. точек разрыва нет.
6) экстремумы функции, промежутки возрастания и убывания
y' = 3x² - 3
3x² - 3 = 0
x₁ = -1; x₂ = 1 - это стационарные точки.
(-∞; -1] y'(x) ≥ 0 функция возрастает
[-1; 1] y'(x) ≤ 0 функция убывает
[1; +∞) y'(x) ≥ функция возрастает
В окрестности точки x₁ = -1 производная функции меняет знак с (+) на (-) -- точка x₁ = -1 - точка локального максимума.
В окрестности точки x₂ = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка локального минимума.
Построение графика (√3≈1.7)
