Предмет: Геометрия,
автор: mika2009rep
Знайдіть радіус кола, описаного навколо трикутника зі сторонами 30см, 56см і 82см
Ответы
Автор ответа:
1
Ответ:
см
Объяснение:
Найти радиус окружности, описанной около треугольника со сторонами 30 см, 56 см и 82 см.
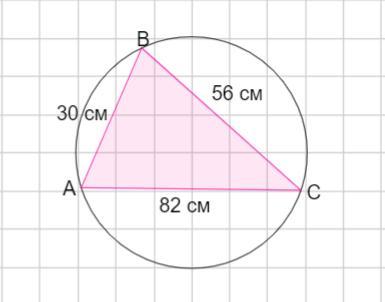
Пусть дан ΔАВС , АВ =30см, ВС =56 см, АС = 82 см.
Найдем радиус окружности описанной около треугольника по формуле:
где a,b,c - стороны треугольника, S - площадь треугольника.
Найдем площадь треугольника по формуле Герона. Для этого найдем полупериметр
и воспользуемся формулой
Значит, площадь треугольника равна 504 см ². Найдем радиус описанной окружности.
Значит, радиус окружности, описанной около треугольника АВС равен.
см
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: karabadztan
Предмет: История,
автор: zenakramarenko924
Предмет: История,
автор: tsyronoki
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Українська мова,
автор: lyalik86