Question

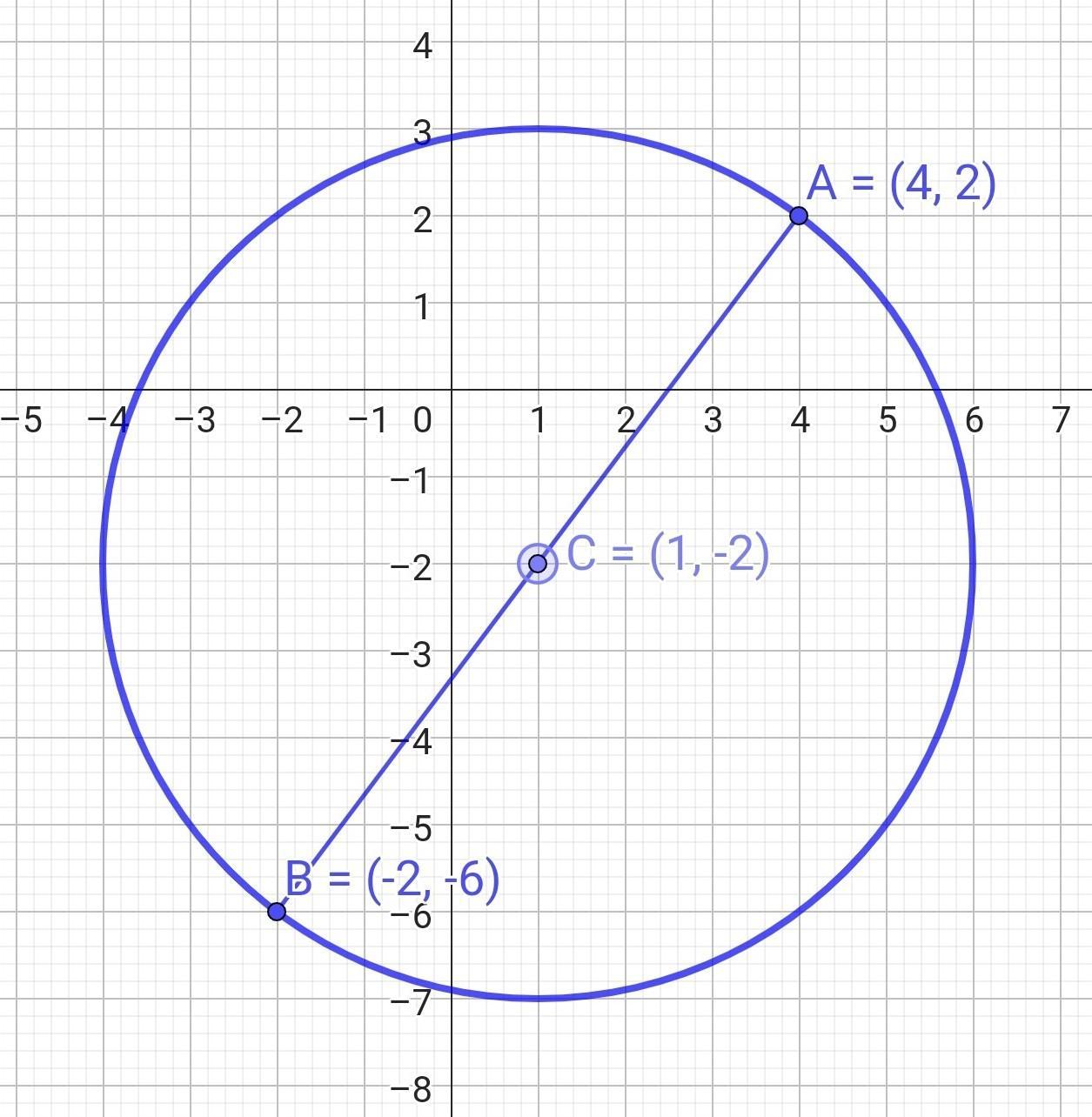
3. Скласти рівняння кола з діаметром АВ, якщо координати точок перетину діаметра з колом:
А(4; 2) і В ( -2; - 6).

Answer 1

Ответ:

Рівняння кола: (x-1)²+(y+2)=25

Объяснение:

Скласти рівняння кола з діаметром АВ, якщо координати точок перетину діаметра з колом:А(4; 2) і В ( -2; - 6).

Рівняння кола з центром у точці (a;b) і радіусом r має вигляд:

(x-a)²+(y-b)²=r²

1.

Знайдемо центр кола (середину діаметра АВ) за формулами:

$\bf x_c=\dfrac{x_A+x_B}{2} ; \;\;\;\;\;\;y_c=\dfrac{y_A+y_B}{2}$

$x_c=\dfrac{4+( - 2)}{2} ; \;\;\;\;\;\;y_c=\dfrac{2+( - 6)}{2} \\ \\ \\ \bf x_c = 1; \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: y_c=-2.$

C(1; -2) - центр кола.

2.

Знайдемо діаметр АВ, як відстань між точками А і В за формулою:

$\bf AB = \sqrt{ {(x_A - x_B)}^{2} + {(y_A - y_B)}^{2} }$

$AB = \sqrt{(4 - ( - 2))^2 + (2 - ( - 6))^2} = \sqrt{ {6}^{2} + {8}^{2} } = \sqrt{36 + 64} = \sqrt{100} = \bf 10$

Радіус кола дорівнює половині діаметра:

r = d/2 = AB/2 = 10/2 = 5

3.

Рівняння кола з центром в точці С(1; -2) та радіусом r = 5:

(x-1)²+(y-(-2))²=5²

(x-1)²+(y+2)=25

#SPJ1