Предмет: Геометрия,
автор: 2009hatyxa2009
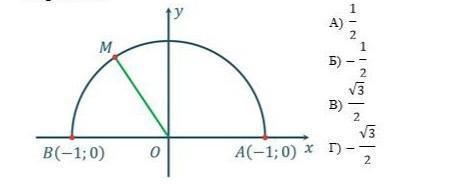
Одиничному колу належить точка M(−1/2
;√3/2). Тоді sin MOA дорівнює:
А)1/2
Б)−1/2
В)√3/2
Г)−√3/2
З ПОЯСНЕННЯМИ!!!
Приложения:
Ответы
Автор ответа:
2
Ответ:
sin∠MOA = √3/2 (B)
Объяснение:
Одиничному колу належить точка M(−1/2; ;√3/2). Тоді sin MOA дорівнює?
- Синусом кута α називають ординату точки М(х; у) одиничного кола.
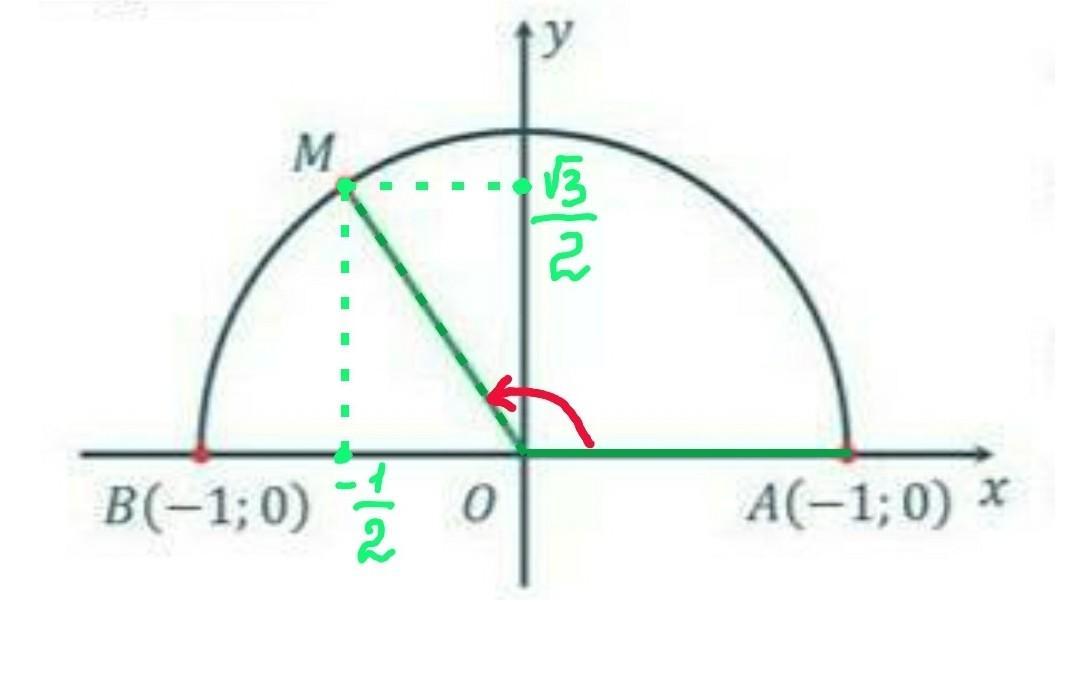
Точка М має координати (-½; √3/2).
Абсциса точки М: -1/2
Ордината точки М: √3/2.
Отже sin∠MOA = √3/2.
Відповідь: В
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: nikagiviva
Предмет: Математика,
автор: aziza777
Предмет: История,
автор: qweriks0
Предмет: География,
автор: artemvingrov
Предмет: Математика,
автор: Аноним