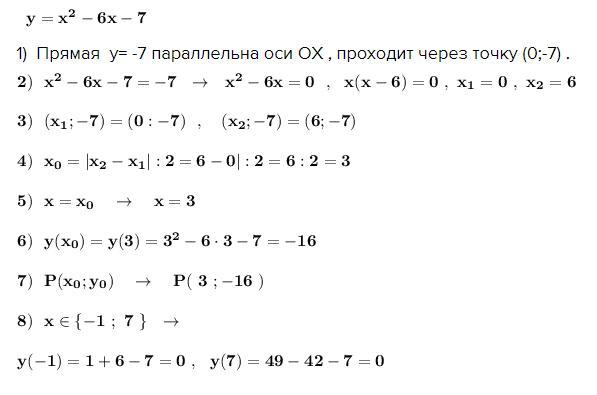Question

помогите пожалуйста срочно математика 9 класс дам 50 баллов

Answer 1

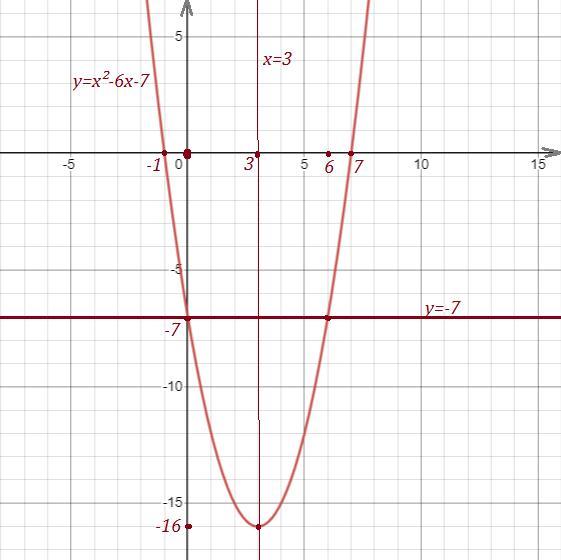
Давайте последовательно выполним каждый из предложенных шагов:1. Проведем прямую у = -7 на координатной плоскости.2. Вычислим корни уравнения \(x^2 - 6x - 7 = -7\):\(x^2 - 6x - 7 + 7 = 0\)\(x^2 - 6x = 0\)\(x(x - 6) = 0\)Таким образом, корни уравнения \(x^2 - 6x - 7 = -7\) равны \(x_1 = 0\) и \(x_2 = 6\).3. Отметим на чертеже точки (0, -7) и (6, -7).4. Чтобы найти абсциссу х₀ вершины параболы, используем корни уравнения: \(x_0 = \frac{x_1 + x_2}{2} = \frac{0 + 6}{2} = 3\).5. Проведем ось симметрии параболы, которая будет проходить через x₀ = 3, и она будет иметь уравнение x = 3.6. Чтобы найти ординату у₀ вершины, подставим x₀ = 3 в уравнение функции \(y = x^2 - 6x - 7\):\(y_0 = 3^2 - 6 * 3 - 7 = 9 - 18 - 7 = -16\).У₀ = -16.7. Отметим на чертеже вершину параболы P(3, -16).8. Теперь, когда у нас есть корни и вершина, вычислим координаты дополнительных точек при x = -1 и x = 7. Подставим их в уравнение функции:При x = -1: \(y = (-1)^2 - 6 * (-1) - 7 = 1 + 6 - 7 = 0\). Точка (-1, 0).При x = 7: \(y = 7^2 - 6 * 7 - 7 = 49 - 42 - 7 = 0\). Точка (7, 0).9. Теперь мы можем нарисовать эскиз графика функции, проходящей через точки: вершина P(3, -16), корни (0, -7) и (6, -7), а также дополнительные точки (-1, 0) и (7, 0). Это парабола, открывающаяся вверх.

Answer 2

Ответ:

 $\bf y=x^2-6x-7$  

1)  Прямая  у= -7 параллельна оси ОХ , проходит через точку (0;-7) .

$\bf 2)\ \ x^2-6x-7=-7\ \ \to \ \ x^2-6x=0\ \ ,\ \ x(x-6)=0\ ,\ x_1=0\ ,\ x_2=6\\\\3)\ \ (x_1;-7)=(0:-7)\ \ ,\ \ \ (x_2;-7)=(6;-7)\\\\4)\ \ x_0=|x_2-x_1|:2=6-0|:2=6:2=3\\\\5)\ \ x=x_0\ \ \ \to \ \ \ x=3\\\\6)\ \ y(x_0)=y(3)=3^2-6\cdot 3-7=-16\\\\7)\ \ P(x_0;y_0)\ \ \ \to \ \ \ P(\ 3\ ;-16\ )\\\\8)\ \ x\in \{-1\ ;\ 7\ \}\ \ \to \\\\y(-1)=1+6-7=0\ ,\ \ y(7)=49-42-7=0$