Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти похідні функцій.
Приложения:
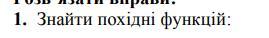
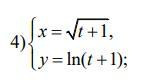
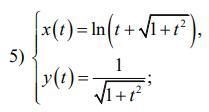
Ответы
Автор ответа:
1
Ответ:
Производные функций , заданных параметрически .
Приложения:
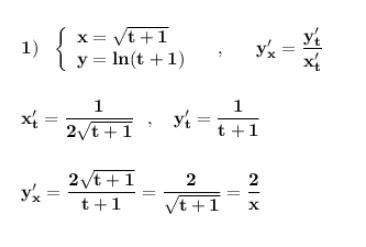
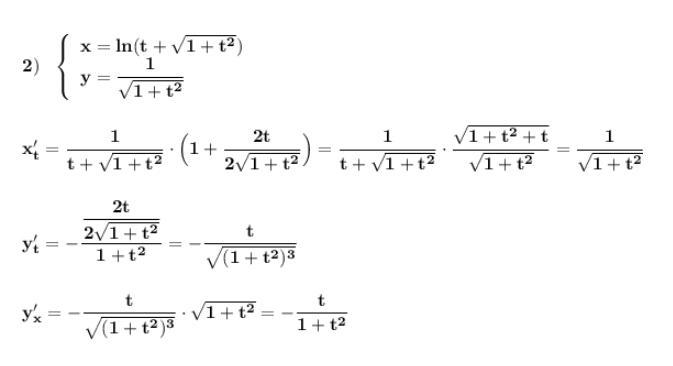
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: География,
автор: nenekrutoi
Предмет: Беларуская мова,
автор: guldanarakhova
Предмет: Химия,
автор: misha2938
Предмет: Қазақ тiлi,
автор: sanatshanbaev
Предмет: Английский язык,
автор: emesusya90