ТЕРМІНОВО!!! ДОПОМОЖІТЬ БУДЬЛАСКА номер 184 і 186
Розпишіть
Буду дуже вдячна!!

Ответы
Ответ:
186)
1) ∠β = 38°; ∠α = 52°; 2) ∠β = 48°; ∠α = 42°;
Объяснение:
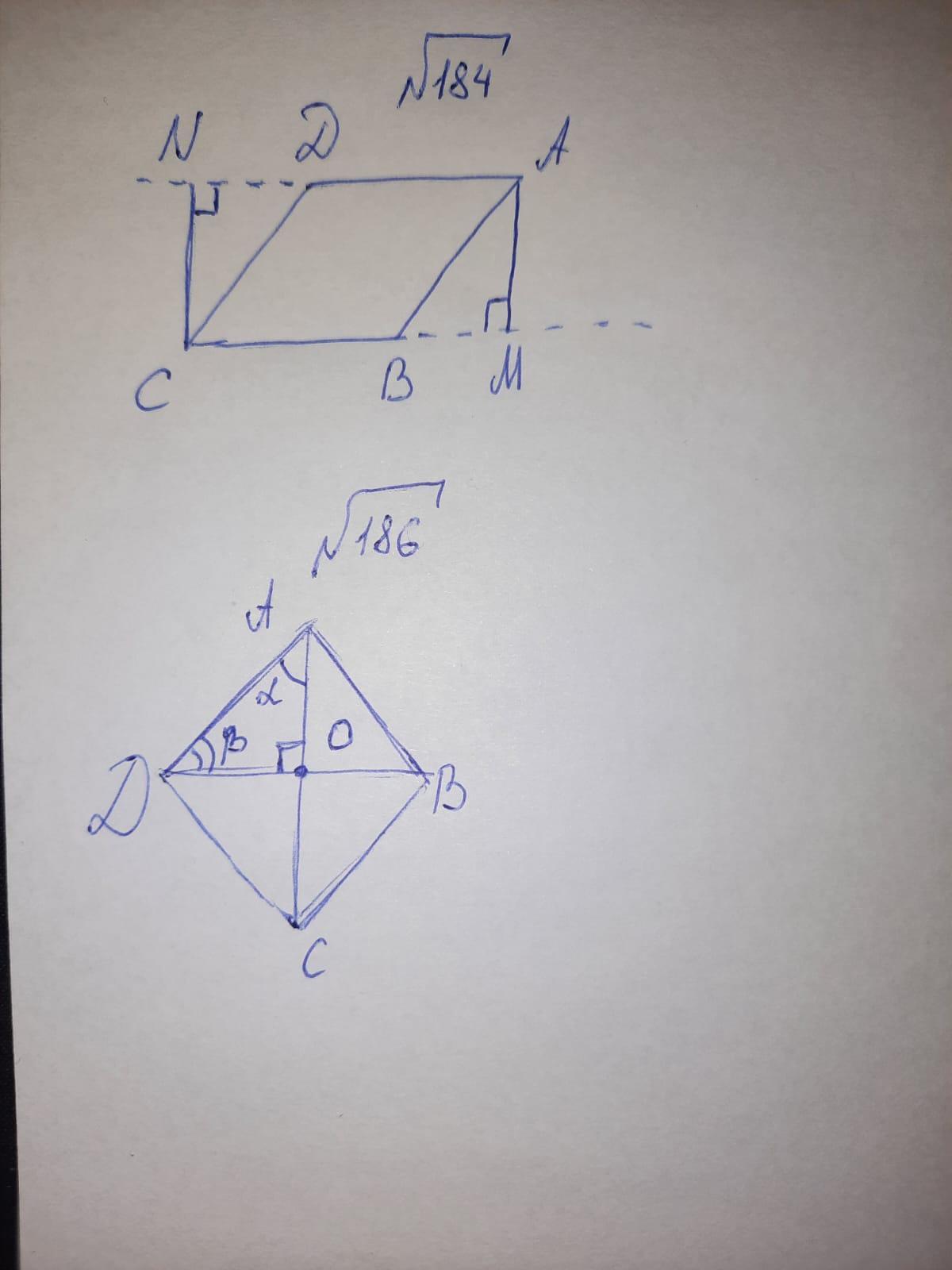
184)
Продлим сторону СВ и проведем к ней высоту АМ. Так как АМ - это высота проведенная к стороне СВ, тогда АМ⊥СM.
Продлим сторону AD и проведем к ней высоту CN. Так как CN - это высота проведенная к стороне AD, тогда СТ⊥ AD.
Рассмотрим четырехугольник AMCN:
Так как АМ⊥СM, значит ∠АМС = 90°
Так как СТ⊥ AD, значит ∠АDС = 90°
Если два угла в четырехугольнике прямые, то этот четырехугольник -- прямоугольник.
Противоположные стороны прямоугольника равны, поэтому AM = CN.
Что и требовалось доказать.
186)
Пусть О это точка пересечения диагоналей. Тогда ∠АОD = 90° (диагонали в ромбе пересекаются под прямым углом).
Рассмотрим треугольник АОD:
Так как ∠АОD = 90°, тогда треугольник АОD -- прямоугольный.
Пусть ∠ОАD = α и ∠ОDA = β, тогда ∠α + ∠β = 90°. Значит, ∠α = 90° - ∠β.
1)
По условию задачи, ∠α - ∠β = 14°.
Составим и решим уравнение:
90 - β - β = 14
-2β = -76
β = 38°
Значит, ∠β = 38°, а ∠α = 90° - ∠β = 90° - 38° = 52°
2)
По условию задачи, ∠α / ∠β = 7 / 8°.
Составим и решим уравнение:
Значит, ∠β = 48°, а ∠α = 90° - ∠β = 90° - 48° = 42°
Ответ: 1) ∠β = 38°; ∠α = 52°; 2) ∠β = 48°; ∠α = 42°;