Предмет: Математика,
автор: cevinmanager
(x+2)(3x-6)(2x+9) ≤ 0
Приложения:
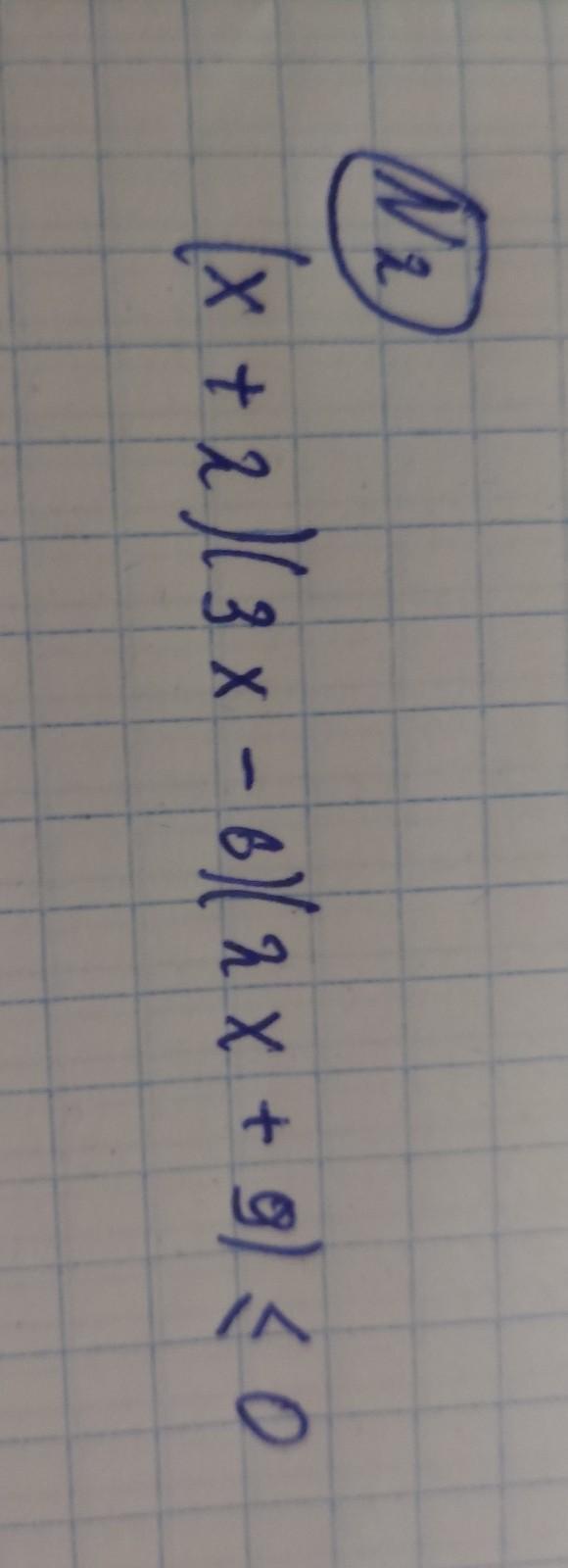
Ответы
Автор ответа:
1
Щоб знайти розв'язок нерівності (x+2)(3x-6)(2x+9) ≤ 0, можемо використати метод інтервалів.
Спочатку знайдемо критичні точки, де вираз (x+2)(3x-6)(2x+9) дорівнює нулю:
x + 2 = 0 => x = -2
3x - 6 = 0 => x = 2
2x + 9 = 0 => x = -4.5
Знайдемо інтервали між цими критичними точками та поза ними.
-∞
znatok228xm:
Там где обозначено будет закрашено
х2=2
[-2;2]
Все?
х3=-4½
можешь на листке показать
тг дай
лучший ответ поставлю ща
@mzhyrko
написал
Автор ответа:
1
Ответ:(-Бесконечность; -4.5] И [-2;2]
Пошаговое объяснение: (x+2)(x-2)(x+4.5)<=0
После обозначаем все 0 на координатной оси Х и выходит так, что (-Бесконечность; -4.5] И [-2;2]
Похожие вопросы
Предмет: География,
автор: tgrisina59
Предмет: Українська мова,
автор: miraignat
Предмет: География,
автор: j47phwhnbz
Предмет: Русский язык,
автор: moldirturganbayeva
Предмет: Математика,
автор: Аноним