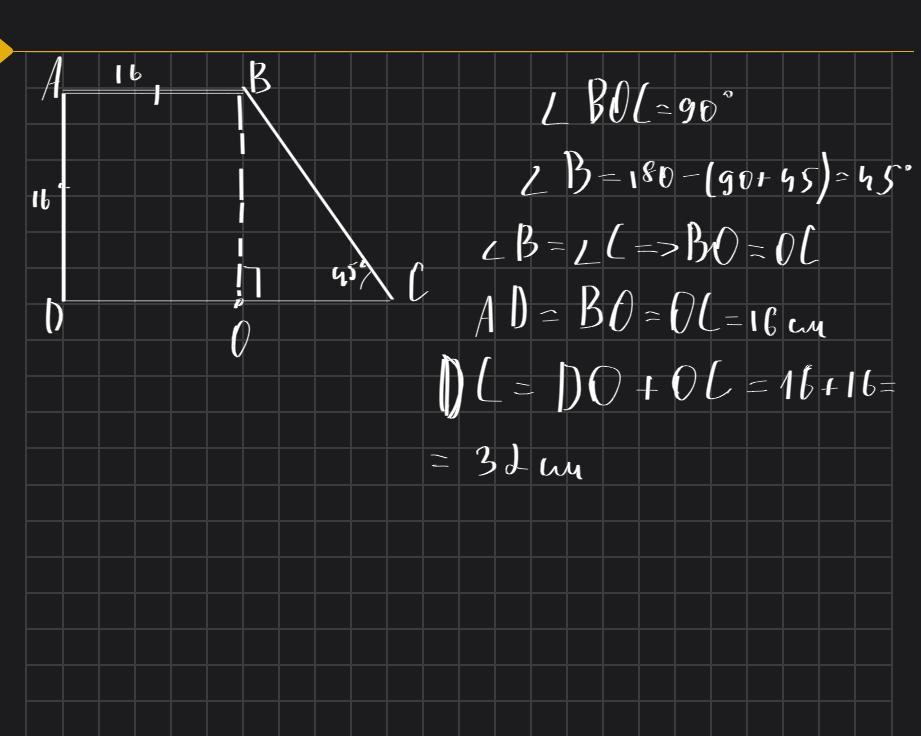в прямоугольном трапеции острый уголь равен 45. Найдите большое основание, если меньшая боковая сторона и меньшее основание равна 16 см.
Ответы
Ответ:
Для знаходження великої основи прямокутної трапеції, якщо меньше основи та одна з менших сторін відомі і гострий кут дорівнює 45 градусів, можна використовувати тригонометричні функції.
Позначимо велике основа як \(B\), менше основу як \(b\), одну з менших сторін як \(a\), та гострий кут як \(\theta\), де \(\theta = 45^\circ\).
Ми знаємо, що \(\tan(\theta) = \frac{a}{B - b}\).
В нашому випадку, \(\theta = 45^\circ\), отже \(\tan(45^\circ) = 1\).
Підставимо це значення і відому довжину сторони \(a\) (яка дорівнює 16 см) в рівняння:
\[1 = \frac{16}{B - b}.\]
Тепер розв'яжемо це рівняння для \(B - b\):
\[B - b = \frac{16}{1} = 16.\]
Тепер, ми знаємо, що \(B - b = 16\).
Оскільки менше основа \(b\) відома (16 см), ми можемо знайти велике основу \(B\):
\[B = b + 16.\]
Підставимо відоме значення \(b\) в це рівняння:
\[B = 16 + 16 = 32.\]
Отже, велике основа трапеції дорівнює 32 см.